Корените на квадратно уравнение

Формула квадратно уравнение корени. Случаите на действителните, многобройни и сложни корени. Факторинг квадратното полином. Геометрична интерпретация. Примери за определяне на корените и factorizations.

основна формула

Помислете за квадратно уравнение:
(1).
Корените на квадратното уравнение (1), определен от формулите:
;.
Тези формули могат да се комбинират както следва:
.
Когато са известни корените на квадратното уравнение, след това полином от втора степен, могат да бъдат представени като продукт на фактори (фактор):
.

След това, ние считаме, че - реалните числа.
Помислете за дискриминантата на квадратното уравнение:
.
Ако дискриминантата е положителна. квадратното уравнение (1) има два различни реални корени:
;.
След разширяването на квадратичен полином факторизиране е от вида:
.
Ако дискриминантата е нула. квадратното уравнение (1) има две множествена (равен) реални корени:
.
Факторинг:
.
Ако дискриминантата е отрицателна. квадратното уравнение (1) има две сложни конюгат корени:
;
.
Ето - имагинерната единица;
и - реални и въображаеми части на корените:
;.
след това

графичен тълкуване

Ако се построи графика на функцията
.
който е парабола, графичния точката на пресичане с оста ще бъде корени на уравнението
.
Когато. графика пресича абсцисата (ос) в две точки.
Когато. Що се отнася до графика оста на абсцисата в един момент.
Когато. графика пресича абсциса.

По-долу са примери на такива графики.

Полезни формули, свързани с квадратно уравнение

Произхода на квадратното уравнение за корените

Ние извършва преобразуване и използване на формула (Е.1) и (F.3):

По този начин, ние имаме формулата за полином от втора степен под формата на:
.
Това показва, че уравнение

се извършва при
и.
Това означава, че са корените на квадратно уравнение
.

Примери за определяне корените на квадратното уравнение

Намерете корените на квадратното уравнение:
(1.1).

Пишем квадратното уравнение в общ вид:
.
Сравнявайки с нашето уравнение (1.1), намираме стойностите на коефициентите:
.
Намираме дискриминантата:
.
Тъй като дискриминантата е положителна. то уравнението има два реални корени:
;
;
.

Следователно ние получаваме разлагането на квадратното полином факторинг:

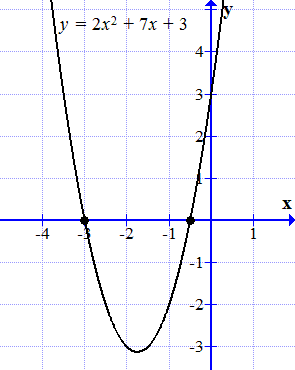
Графиката на у = х 2 + 7 х 2 + 3 пресича хоризонталната ос в две точки.

Ние изграждане на графиката на функцията
.
Графиката на тази функция е парабола. Тя се пресява абсциса (ос) в две точки:
и.
Тези точки са корените на първоначалното уравнение (1.1).

Намерете корените на квадратното уравнение:
(2.1).

Пишем квадратното уравнение в общ вид:
.
Сравнявайки с оригиналното уравнение (2.1), намираме стойностите на коефициентите:
.
Намираме дискриминантата:
.
Тъй като дискриминантата е нула. след уравнението има два множествена (равен) Root:
;
.

След разширяването на трином факторинг е както следва:
.

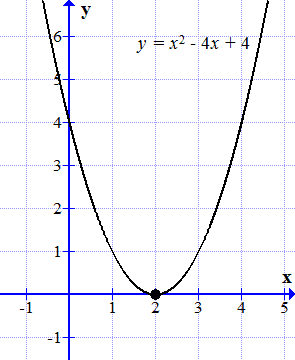
Графиката на у = х 2-4 х + 4 се отнася до абсцисата в точка.

Ние изграждане на графиката на функцията
.
Графиката на тази функция е парабола. То се отнася до абсцисата (ос) в една точка:
.
Тази начална точка е корен на уравнение (2.1). Тъй като този корен е част от факторинг са две:
.
след като корен се нарича множествена. Това е, помисли, че има две еднакви корени:
.

Намерете корените на квадратното уравнение:
(3.1).

Пишем квадратното уравнение в общ вид:
(1).
Препишете първоначалното уравнение (3.1):
.
Сравнявайки с (1), намираме стойностите на коефициентите:
.
Намираме дискриминантата:
.
Дискриминантен е отрицателна. Ето защо, няма реална корени.

Можете да намерите сложни корени:
;
;
.

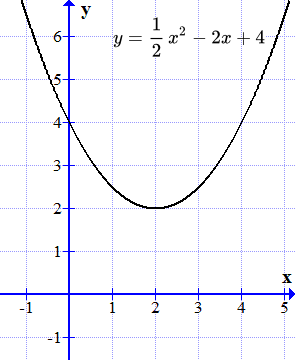
График функция пресича оста х. Не са реални корени.

Ние изграждане на графиката на функцията
.
Графиката на тази функция е парабола. Той не пресича оста х (у-ос). Ето защо, няма реална корени.

Не са реални корени. Корените на комплекса:
;
;
.