Уравнението на допирателната към графиката на функцията

§ 34. уравнението на допирателната към графиката на

В § 32 споменава, че ако точка M (а; е (а)) принадлежи към графиката на функция у = F (х), и ако в този момент на графиката на функцията може да се направи допирателна не е перпендикулярна на оста х, наклонът на допирателната е равна на F '(а). Използваме това няколко пъти. Например, в § 33, беше установено, че графиката на функция Y = грях х (синусоида) в основата прави с ъгъл на наклона на оста х 45 ° (по-точно, допирателна към графиката в основата е положителната посока на ъгъла на оста х 45 °), и пример 5 § 33 точки са открити функцията графика дадено. където допирателната е успоредна на абсцисата. В Пример 2, § 33 се състои уравнение на допирателната към графиката на функция у = х 2 при х = 1 (по-точно в точката (1, 1), но често показва само стойността на абсциса, приемайки, че ако стойността на абсцисата е известно, тогава стойността на ординатата могат да бъдат намерени от уравнението у = е (х)). В този раздел ще се разработи алгоритъм на съставяне на уравнение график kasatelnoy.k всяка функция.

Да предположим, че функция у = F (х) и точка М (а; е (а)), и също така е известно, че има F '(а). Ние изграждане на уравнението на допирателната към функцията графика дадени в дадена точка. Това уравнение, като Уравнение всяка линия не успоредна на оста на ординатата е у = KX + m, така че предизвикателство е да се намери на стойностите на коефициентите к и м.

На пистата има проблем: ние знаем, че а = F '(а). За изчисляване на стойностите на т ние използваме факта, че желаната линия минава през точка M (а; е (а)). Това означава, че ако се замени координати на точка М в уравнението на линията, получи правилния уравнение: е (а) = ка + т, където ние откриваме, че m = е (а) - ка.
Остава да замести стойностите намерени коефициенти китове в линейно уравнение:

Ние получава уравнението на допирателната към графиката на функция у = F (х) при х = а.
Ако, да речем,
Заместването в уравнение (1), получените стойности а = 1, е (а) = 1, F '(а) = 2, ние получаваме: у = 1 + 2 (х-е), т.е. у = 2x-1.
Сравнете този резултат с това, което е получено в Пример 2 на § 33. Естествено, той излезе същото.
Построява уравнението на допирателната към графиката на у = функция TG х в основата. Трябва следователно защото х F '(0) = 1 Заместването в уравнение (1), получените стойности а = 0, F (а) = 0, F' (а) = 1, получаваме: у = х.
Ето защо ние, прекарано tangensoidu в § 15 (вж. Фиг. 62) през началото на ъгъл от 45 ° спрямо хоризонталната ос.
Решаването на тези сравнително прости примери, всъщност използва специфичен алгоритъм, който е включен във формулата (1). Нека да изясним това алгоритъм.

Алгоритъм уравнение допирателна към графиката на функция у = F (х)

1) означава абсцисата на точката на допиране с буквата А.
2) Изчисли 1 (а).
3) Виж F '(х) и се изчислява F' (а).
4) Напълнете с резултатите от, е (а), (а) във формула (1).

Пример 1. Създаване на уравнението на допирателната към графиката на функцията при х = 1.
Решение. Ние използваме алгоритъма, имайки предвид, че в този пример,

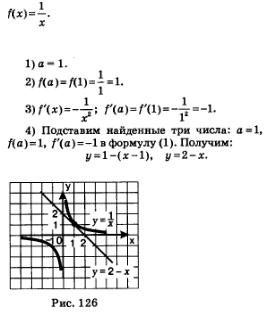
Фиг. 126 показва хипербола. построен направо у = 2.
изчисления тираж показани потвърждава: наистина, у = 2 линия По отношение на хиперболата в точката (1, 1).

A: у = х 2.
Пример 2 Към графика на допирателната така, че да е успоредна на линията Y = 4-5.
Решение. По-точно формулиране на проблема. Изискването за "тангента" обикновено означава "да се уравнението на допирателната." Това е логично, защото ако един човек е в състояние да работят на уравнението на допирателната, че е малко вероятно, че ще има трудности с изграждането в равнината е по права линия от уравнението му.
Ние използваме алгоритъма на съставяне на уравнението на допирателната, имайки предвид, че в този пример, но за разлика от предишния пример, тук има несигурност: не е посочено изрично абсцисата на точката на докосване.
Ние започваме да се говори по този начин. Предпочитан трябва да бъде успоредна на допирателната у = 4-5. Две линии са успоредни, ако и само ако те са ъглови коефициенти. Следователно, наклонът на допирателната линия трябва да бъде равен на наклона на предварително определен права линия: Така стойността на можем да намерите уравнение F "(а) = 4.
В момента има:
Така че от уравнението, има два допирателни удовлетворяващо задача: един в точката с абсциса 2, а другият в точката с абсциса -2.
Сега е възможно да се управляват в съответствие с алгоритъма.

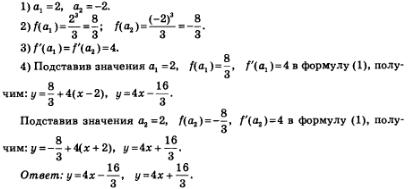
Пример 3. От точка (0; 1) на допирателната към графиката на
Решение. Ние използваме алгоритъма на съставяне на уравнението на допирателната, имайки предвид, че в този пример, имайте предвид, че тук, както в пример 2, не е изрично посочено абсцисата на точката на докосване. Въпреки това, ние сме в качеството на алгоритъма.

Чрез допирателна състояние преминава през точката (0, 1). Заместването в уравнение (2) стойностите на х = 0, у = 1, се получават:
Както можете да видите в този пример, само четвъртата стъпка на алгоритъма успяхме да намерим абсцисата на точката на докосване. Заместването стойност а на = 4 в уравнение (2) добиви:

Фиг. 127 показва геометрична илюстрация на горния пример: изобразените функция

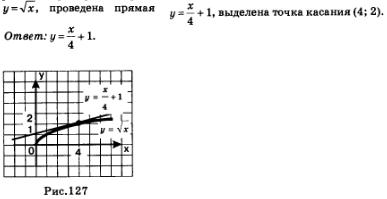
В § 32 се отбележи, че функция у = F (х), производното с фиксирано местоположение х, следните приблизителни уравнение:

За удобство на по-нататъшно обсъждане промените нотация: вместо х и пишем, пишем вместо х а оттам и пишем вместо х-а. След това написано по-горе приблизителното уравнение става:

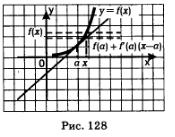
А сега погледнете фиг. 128. Към графика на функция у = F (х) се провежда при допирателна точка М (а; е (а)). Маркирана точка х по абсцисата и близо до него. Ясно е, че е (х) - ординатата на графиката на определена точка х. Какво е е (а) + F '(а), (х-а)? Това допирателна ордината, съответстваща на същата точка х - виж формула (1) .. Какво е значението на приблизителното равенство (3)? Фактът, че за изчисляване на приблизителната стойност на функция приема стойност от тангента на ордината.

Пример 4. Виж приблизителната стойност на цифровата експресия 1.02 7.
Решение. Това е въпрос на намиране на стойностите на функцията Y = х 7 при х = 1.02. Използване на формула (3), като има предвид, че в този пример
В резултат на това, ние получаваме:

Ако използваме калкулатор, получаваме: 1,02 7 = 1.148685667.
Както можете да видите, точността на сближаване е доста приемливо.
Отговор: 1,02 7 = 1,14.

AG Mordkovich Алгебра 10 клас

Ако имате корекции или предложения на този урок, моля свържете се с нас.

Ако искате да видите и другите корекции и предложения за уроци, погледнете тук - Образователен форум.