площ на окръжност

Кръгът се изисква по-внимателен подход и се случи много по-малко работни места B5. Въпреки това, общата схема решения още по-лесно, отколкото в случай на полигоните (вж. Урок "квадрати полигони на мрежата").

Всичко, което се изисква в тези задачи - радиус R. търсене периферна област на кръг може да се изчислява след това по формулата S = πR 2. Освен това от тази формула, която е достатъчна, за да се намерят решения за R 2.

За тези стойности, достатъчно е да обикаля точка, разположена в пресечната точка на линиите на мрежата. И след това да използвате питагорова теорема. Обърнете внимание на конкретни примери за изчисляване на радиус:

Задача. Намерете радиусите на трите кръга, показана на фигурата:

Изпълнение допълнителни конструкции във всеки кръг:

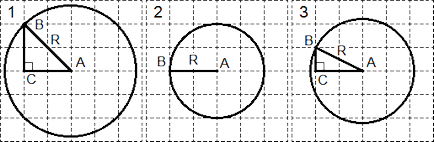
Във всеки случай, точка Б на обиколката е избран така, че да лежи в пресечната точка на линиите на мрежата. Точка С в кръговете 1 и 3 са допълващи към формата на правоъгълен триъгълник. Остава да намерим радиусите:

Помислете триъгълника ABC в първия кръг. Чрез Питагоровата теорема: R2 = AB 2 = AC + BC 2 2 = 2 2 + 2 2 = 8.

За всички очевидно втория кръг: R = AB = 2.

Третият случай е подобен на първия. От триъгълник ABC Питагоровата теорема: R2 = AB 2 = AC + BC 2 2 = 1 2 + 2 2 = 5.

Сега ние знаем как да се намери радиуса на кръг (или поне да му квадрат). И затова, ние можем да намерим района. Има задачи, които изискват сектора да намерите областта, а не цялата гама. В такива случаи е лесно да се разбере каква част от условията на този сектор, и по този начин да се намери в района.

Задача. Намерете площ S на сенчестия сектор. В отговора си S / π.

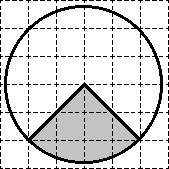
Очевидно е, че този сектор се пада една четвърт от окръжност. Следователно, S = 0,25 · S кръг.

Остава да намерите набор от S - площ на кръг. За да направите това, изпълнете допълнително строителство:

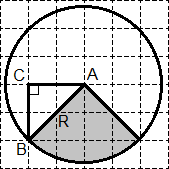
Правоъгълна - ABC триъгълник. До питагорова теорема, ние имаме: R 2 = AB 2 = AC + BC = 2 2 2 2 2 + 2 = 8.

Сега ние откриваме областта на кръг и сектори: S = кръг πR 2 = 8 π; S = 0,25 · S кръг = 2 π.

Накрая, желаният стойност е равна на S / π = 2.

Площта на сектора на неизвестно радиус

Добрата новина е, че такива проблеми - най-лесният на всички задачи в областите, които са в изпита по математика. В допълнение, кръга и сектора винаги се поставя върху мрежата. Ето защо, за да научите как да се реши тези проблеми, просто погледнете на снимката:

Да предположим, че първоначалното кръг има площ S = колело 80. След това може да бъде разделен на два сектора, площ S = 40 всяка (вж. Стъпка 2). По подобен начин, всеки от тези sektorov- "половини" може да бъде разделена на две отново - получаване на четири сектора S = 20 всяка област (виж етап 3.). Най-накрая, че е възможно да се разделят всеки един от тези сектори, за двама - 8 получите sektorov- "бучки". Площта на всеки от тези "бучки" ще бъде S = 10.

Забележка: малък дял на всеки един проблем на изпита по математика не е! Така, алгоритъмът за В-3, както следва:

1. Нарежете на оригиналния кръга в 8 sektorov- "бучки". Площта на всеки един от тях е точно 1/8 от площта на целия кръг. Например, ако състоянието на колелото има кръгла площ S = 240, тогава "бучки" са S = 240. 8 = 30 област;
2. Разберете колко "отпадъци" се намира в начален сектор на областта, която искате да търсите. Например, ако ни сектор се поставя 3 "бучки" 30, желаната област на сектора е равна на S = 3 х 30 = 90. Това ще бъде отговор.

Това е! Проблемът е решен почти устно. Ако все още не разбирате нещо, купи пица и го нарежете на 8 парчета. Така, всеки детайл ще sektorom- "бучки", които могат да се комбинират в по-големи парчета.

А сега погледнете образец на тест изпита:

Задача. На милиметрова хартия се направи кръг, чиято площ е равна на 40. Виж областта на защрихованата фигурата.

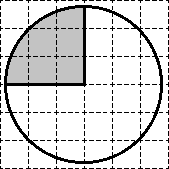
Така областта на окръжност е равен на 40. го разделя на 8 сектори - всяка област S = 40. 5 = 8. получаване на:

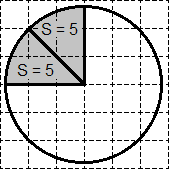
Ясно е, че сенчести сектор се състои от точно две sektorov- "отпадъци". Следователно, с площ, равна на 2 · 5 = 10. Това е всичко, решение!

Задача. На милиметрова хартия начертайте кръг, чиято площ е равна на 64. Намерете областта на сенчестата фигурата.

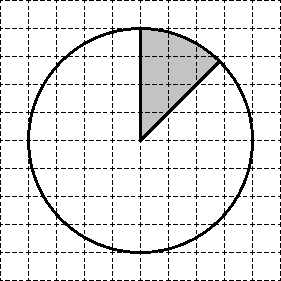
Отново се разделят на цялата окръжност на 8 еднакви сектори. Ясно е, че площта на един от тях просто искате да намерите. Следователно, площта му е S = 64. 8 = 8.

Задача. На милиметрова хартия начертайте кръг, чиято площ е равна на 48. Намерете областта на сенчестата фигурата.

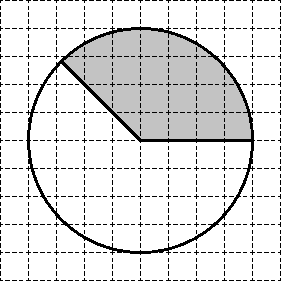
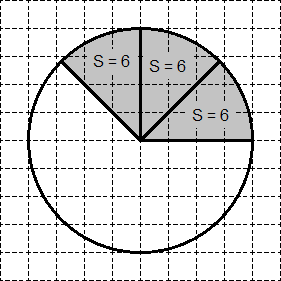
Отново се разделят на кръга в 8 еднакви сектори. Площта на всеки един от тях е равно на S = 48. 8 = 6. В иска сектор е поставен точно три sektora- "бучки" (вж. Фигура). Следователно, областта на желания сектор 3 х 6 = 18.

• Безплатна Подготовка за изпита 7 прости, но много полезни уроци + домашна работа
•