Ntsialnaya и нормална компонента на ускорението

Тангенциални и обичайните компоненти на ускорение

Ускорение - вектор количество характеризиране на скоростта на движещо се тяло се променя скоростта на големина и посока.

Средните точки ускорение в АТ на интервал от време е вектор ASR. δV е равен на съотношението на нарастване на вектора на скоростта на интервал АТ.

Ускорение (моментално ускорение) на точката се нарича вектор количество на. равна на първо производно на скоростта V на по отношение на времето (секунди или производно на радиуса - вектор, с течение на времето).

ускорение в момент равен на граничната точка средно ускорение по време на

В декартова координатна система, векторът може да се запише по отношение на нейните координати:

вектор ускорение единица

Векторът може да бъде представена като сумата от два компонента:

- тангенциалната компонента на ускорението е насочено по допирателната към траекторията на точката и е равна на

където векторът - допирателната на единичен вектор, изготвен в точка на траекторията и посоката на скоростта

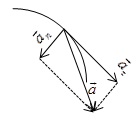
Вектори и codirectional с равномерно ускорено движение; по това когато движението ravnozamedlennom.

Тангенциална ускорение - характеризира степента на промяна на модул на вектора на скоростта на точката (характеризира скоростта на промяна в размера).

За равномерно движение.

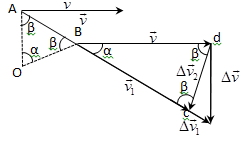
-нормална компонента на ускорението (ускорението) е насочена по нормалата към траекторията и точката счита по посока на центъра на кривината на траекторията. Крива траектория може да бъде представена като поредица от елементарни части, всяка от които може да се разглежда като дъга от окръжност с радиус R (радиус на кривина наречен дадена точка на кривата траектория в обиколка)

Нормално ускорение характеризира степента на промяна на посоката на вектора на скоростта (показва промяната на скоростта на посоката).

пълен модул ускорение:

Класификацията зависи от движението на тангенциални и нормални компоненти:

§5 Кинематика на въртеливо движение

Въртене на тялото при φ ъгъл може да се опише чрез вектор, чиято дължина е равна на МФ. и посока съвпада с оста на въртене и определя от правилото дясната винт (палеца, отдясно):

Четири пръста на дясната си ръка - посоката на въртене, огънатата палеца показва посоката на вектора.

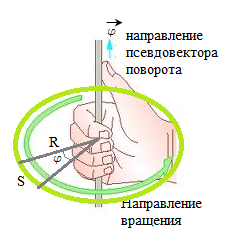
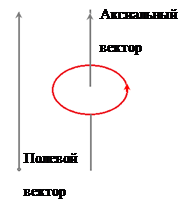
Посоката на въртене на вектор Ф е, е свързано с посоката на въртене на правилото на дясната страна. Такива вектори са посочени като аксиален (аксиална) или pseudovectors да ги отличават от нормалните (понякога се нарича поле) вектори. Това е вектор ъгловата скорост, която е числено равно на първата производна на ъгъла на въртене по отношение на времето и т е насочено по фиксирана ос на принципите на дясната ръка.

Ъгловата скорост. както и вектор аксиален. Аксиални вектори имат определени точки на приложение, те могат да бъдат депозирани от всяка точка на оста на въртене. Често те лежеше на фиксирана точка на ос на въртене, в началото на получения доклад едновременно координатна система. въртене на тялото се нарича хомогенен, ако.

Скоростни точки в контраст с ъгловата скорост. орган, наречен линейна скорост. То е насочено перпендикулярна на оста на въртене (т.е. вектор) и радиус на - вектор R. conected до точка Р от центъра на кръга О и равен на вектор продукта от:

Uniform въртене може да се характеризира периода на въртене T, чрез който да се разбере времето, в което тялото прави един оборот, т.е. върти. След това - връзката на ъгловата скорост с обръщение период.

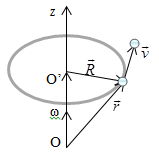
честота на въртене - броя на оборотите за единица време; ,

В случай на променлив въртеливото движение на ъгловата скорост на материал, а не се променя, както в количество и посока. За да се характеризира степента на промяна на ъгловата скорост на неравномерното въртене около фиксирана ос се добавя вектор ъглово ускорение на тялото равна на първата производна на неговата ъглова скорост във времето.

Векторът също е аксиален (или pseudovector). Вектори и codirectional с ускорено въртене () и противоположно насочено с бавно въртене.

()

Ускоряване на произволна точка Р на тялото за разлика от ъгловото ускорение на тялото се нарича линейно ускорение.

За равномерно ускорено въртеливо движение могат да бъдат написани:

Връзка на линейни и ъглови измервания: