Коефициентът на ковариация и корелация
Преди диаграма на разсейване бе обсъдено, илюстрираща разпределението на двуизмерни цифрови данни (вж. Последната част на двумерен представяне на изображението на цифрови данни числени данни бележки под формата на таблици и диаграми). В тази статия ще разгледаме две количествени показатели, характеризиращи отношенията власт между двете променливи - ковариацията и корелационен коефициент. [1] ковариация изчислява поради линейна връзка между две числови променливи X и Y. ковариация на пробата:
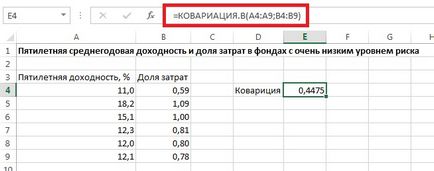
Фиг. 1. добив Средната петгодишен, а делът на разходите за взаимни фондове с много нисък риск
Любопитно е, че ковариация на случайна променлива с вариация, равна на:
Ако ковариацията е положителен, с увеличаване на стойностите на случайна променлива, втората стойност, води до увеличаване, и ако знакът е отрицателен - това намаление. Въпреки това, само абсолютната стойност на ковариацията е невъзможно да се прецени колко от стойността на свързани помежду си, тъй като това зависи от мащаба на тяхното разпространение. Scale да нормализират чрез разделяне на продукта от стойността на ковариация стандартно отклонение (квадратен корен на вариацията). Така се получава така наречения коефициент на корелация на Пиърсън.
В зависимост от относителната сила или връзката между двете променливи, съставляващи двумерен проба измерва коефициента на корелация, която варира от -1 до идеалното обратно пропорционално на един за перфектно директна пропорция. Коефициентът на корелация е обозначен с гръцката буква р. Линейността на връзката означава, че всички точки, показани на разсейване на графиката, лежат на една права линия (Фигура 2). Панел А показва линейна зависимост между променливите X и Y. Така, р корелационния коефициент е равен на 1, т.е. когато X увеличава променливи, Y намалява променлива. Панел В показва ситуация, в която между променливите х и у имат корелация. В този случай, р корелационния коефициент е равен на 0, а когато променливите X увеличава, Y променлива не показва определена тенденция: тя нито намалява, нито се увеличава. Панел В показва пряка връзка между линейни променливи X и Y. Следователно, р корелационния коефициент е равно на 1, и, когато променливите X увеличава, Y променлива също се увеличава.
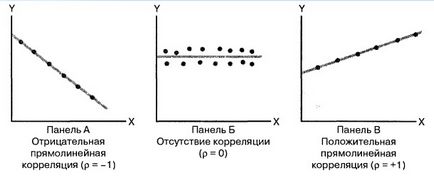
Фиг. 2. Три вида на връзката между две променливи
При анализа на проби, съдържащи двумерен коефициент на корелация на данни изчислява проба, която е означена с буквата R. В реални ситуации коефициента на корелация се рядко-точни стойности -1, 0 и +1. Фиг. 3 показва диаграми шест разсейване и съответстващите корелационни коефициенти R между променливите 100 X и Y.
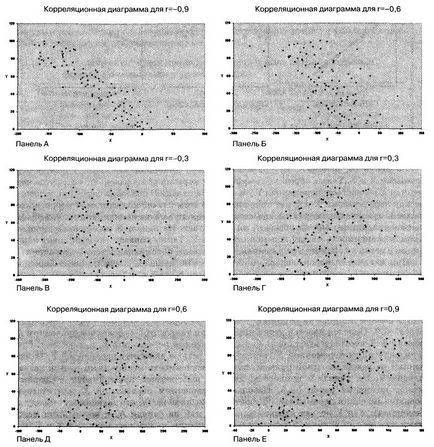
Фиг. 3. Шест разпръсна диаграми и съответните коефициенти на корелация, получени чрез програма Excel
Панел А показва ситуацията, в която проба коефициент на корелация г е равно на -0.9. Наблюдава се ясна тенденция: малки стойности на X отговарят на много високи стойности на променливата Y, и обратно, големи стойности на X съответстват на малки стойности на променливата Y. Въпреки това, данните не лежат на една права линия, така че връзката между тях не може да се нарече линейна. Панел В показва коефициент проба данни корелация между тях е равно на -0,6. Малките стойности на X съответстват на големи стойности на променлива Y. Имайте предвид, че отношенията между променливите х и у на не могат да бъдат наречени линейна, както в панел А, и връзката между тях не е толкова голяма. Коефициентът на корелация между променливите х и у, посочена в панел В, равно на -0.3. Наблюдава се лека тенденция, според която големи стойности на променливата X, като цяло съответстват на малки стойности на променливата Y. панели D-F илюстрират положителни корелации между данни - ниски стойности на променливите X съответстват на големи стойности на променливата на Y.
Обсъждането на фиг. 3, използвахме термина тенденция, тъй като между променливите х и у не причинно-следствени най. Корелацията не означава причинно-следствена връзка между променливите х и у, т.е. промяна на стойността на една променлива не е задължително да доведе до промяна в стойността на друг. Силната корелация може да бъде произволен и трета променлива съотнасяше остава извън анализа. В такива ситуации е необходимо да се проведат допълнителни изследвания. По този начин, може да се твърди, че причинно-следствени връзки генерират корелация, но корелацията не означава причинно-следствени връзки.
Селективна коефициент на корелация:
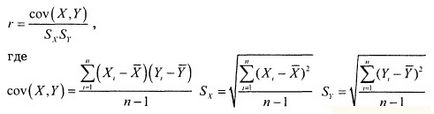
Както се използва Excel функция CORREL = () (Фиг. 4) за изчисляване на коефициента на корелация.
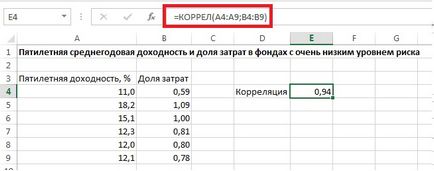
Фиг. 4. функция CORREL в Excel
По този начин, коефициента на корелация показва линейна връзка или връзка между двете променливи. близо коефициент на корелация е да -1 или 1, по-силен е линейна връзка между две променливи. Знакът на коефициента на корелация определя от естеството на връзката: директно (+) и назад (-). Силна корелация не е причинно-следствена връзка. Това само показва тенденция характеристика на извадката.