Как да се намери уравнението на допирателната към графиката на

Допирателната към кривата - линия, която е в непосредствена близост до тази крива в дадена точка, т.е. простира през него, така че малка площ около тази точка е възможно без много загуба на точност да се замени крива сегмент на допирателната. Ако тази крива е графика на функцията, допирателната към възможно е да се изгради специална уравнение.

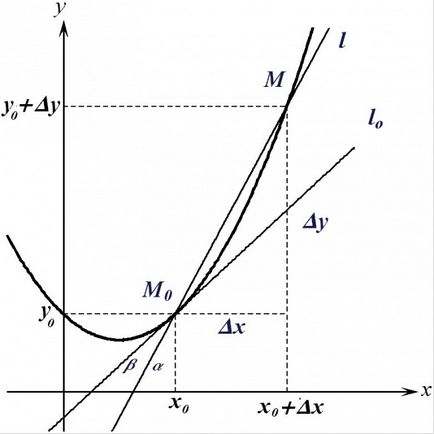
Да предположим, че имате графиката на функция. Две точки от тази графика, можете да черпят права линия. Такава линия пресича графика дадена функция в две точки, наречен пресичане.

Ако, оставяйки първата точка на земята, постепенно се премести на втората точка към нея, пресичащия ще се завърти бавно, с тенденция към всяка конкретна позиция. В крайна сметка, когато двете точки се сливат в едно, сегмент да прилягат плътно в графика си в тази една точка. С други думи, пресичащ на свой ред да тангента.

Всяка наклонена (т.е. не вертикална) линия на координатната равнина е графиката на уравнението у = KX + б. Secant, минаваща през точките (x1, y1) и (2 бр, y2), като по този начин трябва да отговарят на следните условия:
KX1 + б = Y1, kx2 + б = Y2.
Решаването на тази система от две линейни уравнения, получаваме: kx2 - KX1 = y2 - y1. По този начин, к = (y2 - y1) / (х2 - х1).

Когато разстоянието между x1 и x2 на нула, разликата в завой диференциали. По този начин, в уравнението на допирателната преминаващ през точката (x0, y0) коефициент к е равно ∂y0 / ∂x0 = F '(x0), т.е. стойността на производно на F функция (х) при x0.

За да се научат коефициент б, заменен вече изчислената стойност на к в уравнение F "(x0) * x0 + б = F (x0). Решаването на това уравнение по отношение на В, ние откриваме, че б = F (x0) - F '(x0) * x0.

Окончателният вариант на уравнението на допирателната към графика дадена функция в точка x0, е както следва:
Y = F '(x0) * (х - x0) + F (x0).

Като пример, помисли уравнението на допирателната към F функция (х) = х ^ 2 в точка x0 = 3. производно с х ^ 2 е 2x. Следователно, уравнението на допирателната става:
у = 6 * (х - 3) + = 9 6x - 9.
Валидността на това уравнение е лесно да се провери. Графика линия у = 6х - 9 преминава през същата точка (3; 9), и че първоначалното парабола. Като изгради двете графики, можете да видите, че това е наистина пряк контакт с параболата в този момент.

По този начин, графиката на функцията е допирателна на x0 точка само когато функцията е производно на този етап. Ако функцията за точка x0 има прекъсване на втория вид, става ясно допирателната към вертикална асимптота. Въпреки това, самото съществуване на производната в точка x0 не гарантира необходимата съществуването на допирателната в този момент. Например, F функция (х) = | х | в точка x0 на = 0 е непрекъсната и диференцируема, но допирателна към него в този момент е невъзможно. Стандартната формула в този случай дава уравнение у = 0, но тази линия не е допирателна към модула графики.

• Математика за ученици - уравнението на допирателната
• Напишете уравнението на допирателната

При съставянето на уравнението на допирателната към графиката на понятието "абсциса на точката на контакт." Тази стойност може да се настрои първоначално в условията на проблема, или трябва да се определя самостоятелно.

Равен лист за клетка координатните оси х и у. Разглеждане на даден уравнението за графиката на функцията. Ако тя е линейна, е достатъчно да се знае две стойности за у параметър за всички х, а след това изгради тези точки върху координатните оси, и да ги свърже с права линия. Ако графиката на нелинейна, а след това направи таблица в зависимост от х и вземете най-малко пет точки за заговор.

Построява се функцията и да се установи предварително определена координатна ос на допирната точка. Ако тя съвпада с функцията, неговата х-координата е равна на буквата "а", която се обозначава с абсцисата на точката на докосване.

Определяне на стойността на точката на докосване абсциса за случая, когато заданието не съвпада с допирателната функция графика. Изберете третата опция е буквата "а".

Запишете уравнение функция е (а). За да направите това, оригиналното уравнение за х и заместител. Виж производното на F функция (х) и F (а). Замести необходимите данни в общото уравнение на допирателната, която има формата: у = е (а) + F '(а) (х - а). В резултат на това уравнение, което се състои от три неизвестни параметри.

Сложете го на мястото на х и у координати на дадена точка, през която тангента. След това се намери решение на уравнението, получена за всичко. Ако тя е квадратна, ще има две стойности на точката за абсциса докосване. Това означава, че допирателната се провежда два пъти в близост до графиката на функцията.

Равен графика на дадена функция, и успоредна на линията, което също е състоянието на проблема. В този случай също така определя като неизвестен параметър и заменен в уравнение е (а). Равнява производно е (а) производно на уравнение успоредна линия. Това действие идва от състоянието на паралелизъм на двете функции. Виж корените на получената уравнение, което ще бъде абсциси точката на допиране.

Директен у = е (х) е допирателна към графиката, показана на фигура при x0 в случай, че той преминава през точката (x0; F (x0)) и има ъглово коефициент F '(x0). Намерете коефициент знаейки, особено тангента на мига.

• - математически справочник;
• - молив;
• - тетрадка;
• - транспортир;
• - на компасите;
• - писалка.

Имайте предвид, че графиката на диференцируема функция на x0 е (х) е същият като сегмента на допирателната. С оглед на това, че е достатъчно близо до дължина L, която преминава през точката (x0; F (x0)) и (x0 + Δx; F (x0 + Δx)). За зададени права линия, която преминава през определена точка А с коефициенти (x0; F (x0)), трябва да се посочи му наклон. Ъгловата коефициент е Δy / Δx сечащ допирателна (ьН → 0) и тенденция към F номер "(x0).

Ако не съществуват стойностите на F '(x0), или не тангенциален, или тя се простира вертикално. С оглед на това, наличието на производната на функцията на x0 поради наличието на не-вертикална тангента в контакт с функцията на график в точката (x0, F (x0)). В този случай, на ъгъла е допирателна коефициент е е '(x0). По този начин, става ясно, геометричен смисъл на производното - изчисляване на наклона на допирателната.

Равен на фигура допълнителни допирателните които ще влязат в контакт с графиката на функцията в точки X1, Х2 и Х3, и проверка на ъглите, образувани от тези допирателна с абсцисата (ъгълът се отчита в положителна посока от оста на допирателната линия). Например, първият ъгъл, т.е. α1, ще бъде остър, втората (алфа2) - тъп, а третият (а3) е нула, тъй като допирателна линия, очертана успоредно на говедото на ос. В този случай тъп ъгъл допирателната - отрицателна стойност, допирателната малък ъгъл - положително, и ако резултатът е нула tg0.

Правилно определи ъгълът, образуван от допирателната. За да направите това, използвайте транспортир.

Две прави линии са склонни паралелно ако техните ъглови коефициенти са равни помежду си; перпендикулярно, ако продуктът на ъгловите коефициенти на допирателната е -1.

• Допирателната към графиката на функцията

Преди да се пристъпи към определяне на координатите на точката на докосване, проверка на възможността за допирателна. За тази функция анализ, който описва определена крива на определено място.

допирателната към произволна самолет в правоъгълна координатна система - е границата, до която има тенденция да сечащ тази крива в най-близко разстояние на точки на пресичане на кривата и правата линия.

Следователно, тангента има само една обща точка на кривата. Все пак, това твърдение е вярно за добре дефинирана област. В зависимост от поведението на кривата в другите области на координатната равнина, допирателната линия може да се пресичат предварително определено или обратно, далеч от него.

Някои криви може да се направи допирателна във всяка точка. Примери на такива линии - кръг, елипса. Други непрекъснати криви могат да бъдат точката, в която не е възможно да се конструира допирателната. Той се среща в райони, където напречното не се стремят към една и съща граница позиция.

Да предположим, че произволна крива е описана от израза Y = F (х). Общата форма на уравнение права Y = KX + а. Очевидно е, че в точката на допиране с координатите (XO, YO) уравнението: F (Хо) = kXo + а.

Ако функцията F (х) е диференцируема в точката Хо, в този момент може да се направи допирателна към кривата и наклона на допирателната към оста ОХ е стойността на функцията производно: К = F '(Хо). Уравнението на допирателната в точката на контакт става Йо = F '(Хо) * Хо + а. Проблемът за намиране на координатите на точката на допир се редуцира до решаване на система от две уравнения с две неизвестни Йо = F (Хо) и Йо = F '(Хо) * Хо + а.

Самолетът е допирателна към повърхността, ако повърхността има обща точка и по права линия или плоска крива. Определяне на координатите (Хо Йо Zo) обща точка на допирателната равнина на извитата повърхност и целевата Z = F (х, у) е възможно, ако функцията F (х, у) има пълна диференциална в тази точка.