Физика и математика клас

Пирамида нарича полихедронов изправена пред една от които е произволен многоъгълник, а от другата страна - триъгълници с общ връх.

Перпендикулярна съставен от върха на пирамидата на основната равнина, наречен височината на пирамидата.

Tetrahedron - пирамида, чиято основа е триъгълник.

Триъгълници, които съставляват тетраедър, наречени лицата си. своя страна - ребра. и на върха - на върха на тетраедър. Две краища на тетраедър като няма общи върхове се наричат ​​обратното. Обикновено, изолиран от един Tetrahedron ръбове и нарича основата му. и останалите лица се наричат ​​странични повърхности.

Редовен тетраедър се нарича тетраедър, чийто всички ръбове са равни.

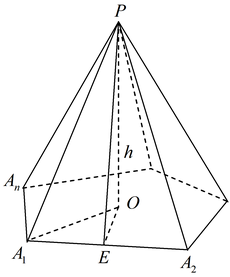
Правилно нарича тази пирамида пирамида, ако основата му - правилен многоъгълник, а базовата височината на пирамидата съвпада с центъра на многоъгълника. Line, съдържащ правилната височина на пирамидата се нарича ос.

Височината на страничната стена на редовен пирамида, изготвен от горната му част, наречена Апотема.

Пресечена пирамида (вж. По-долу) е правилно. ако това се получава редовна пирамида сечение равнина, успоредна на основата. База десен пресечена пирамида - редовни полигони и странични лица - равнобедрен трапец. Височината на трапецовидна нарича Апотема пресечена пирамида.

Обмислете следните твърдения:

Страничните ръбове на пирамидата са равни.

Страничните ръбове на пирамидата са еднакво наклонени към основата на пирамидата.

На върха на пирамидата се очаква в центъра на кръга окръжност около основата на пирамидата.

Височините на страничните стени на пирамидата, извлечени от върха на пирамидата, са равни, а височината на пирамидата е в рамките на пирамидата.

Всички двустенни ъгли в основата на пирамидата са равни.

На върха на пирамидата се очаква в центъра на кръга вписан в основата на пирамидата.

Редовното триъгълна пирамида противоположни ръбове двойки перпендикулярно.

Ако страничните ръбове на пирамидата са равни, тогава основата е правилен многоъгълник, около която може да се опише от кръг, и на върха на пирамидата се очаква в центъра на този кръг.

Ако двустенните ъгли в основата на пирамидата са равни, тогава основата на пирамидата е многоъгълник, който може да бъде вписан в окръжност и връх на пирамидата се очаква в центъра на този кръг.

Приложенията 1, 2, 3, 4, 5, 6, са еквивалентни.

Напречното сечение на пирамидата от равнина, успоредна на основата

Напречното сечение на пирамидата от равнина, успоредна на основата (перпендикулярно височина) разделя височината и страничните ръбове на пирамидата в пропорционални сегменти.

Напречното сечение на пирамидата от равнина, успоредна на основата (перпендикулярно височина) има многоъгълник-като основата на пирамидата, и коефициента на сходство на полигони е равен на съотношението на техните разстояния от върха на пирамидата.

Квадратни сечения успоредни на основата на пирамидата са както квадрати на техните разстояния от върха на пирамидата.

Повърхностната площ и обем на пирамидата

Да предположим, че - височината на пирамидата, - периметъра на основата на пирамидата, - базовата площ на пирамидата, - страничната повърхност на пирамидата, - общата площ на пирамидата, - обем на пирамидата. Тогава ние имаме следните зависимости:

Ако всички двустенни ъгли в основата на пирамидата са равни, и височините на всички странични лица на пирамидата, извлечени от върха на пирамидата, са равни,