Уравнението на допирателната и нормално уравнението на графиката на
Tangent - е директно. който се отнася до функцията на графиката в една точка и всички точки, които са най-близо до графиката на функцията. Ето защо, допирателната работи на графиката на определен ъгъл и не може да премине през точката на допиране на тангенти няколко различни ъгли. Уравнения допирателна и нормално уравнение на графиката съставен използва производно.
Уравнението на допирателната е получено от уравнението на линията.
Ние се получи уравнението на допирателната, а след това - на нормалното уравнение на графиката на функцията.
Припомнете си уравнение на линия с наклон:
В него K - склона.
Следователно ние получаваме следната позиция:
Стойността на производно F '(х 0) на функция у = F (х) при 0 х е равно на к наклон = tgφ допирателна към графиката изтегля през точка M 0 (х у 0. 0). 0, когато Y = F (х 0). Това е геометричното значение на производно.
По този начин, ние може да замени к от F '(х 0) и след уравнение допирателната към графиката на функцията:
Задачите за подготовка на уравнението на допирателната към графиката на функцията (и скоро ще преминем към тях) се изисква да донесе по-горе дава формулата за полученото уравнение на права линия по общ начин. За да направите това, всички от букви и цифри, за да бъде преместен в лявата страна на уравнението, а в дясната част на левия нула.
Сега, за нормалното уравнение. Нормално - това е права линия, преминаваща през точката на контакт перпендикулярна на графиката на допирателната. Нормално уравнение:
Ние се обръщаме към примерите. За решения изискват таблица на производни (отваря се в нов прозорец).
Пример 1. Създаване на уравнението на допирателната и нормално уравнението на графиката на функцията ако абсцисата на точката на допиране.
Решение. Намери ордината допирна точка:
Нека да намерите производната на функцията:
Намираме стойността на производното в точката на контакт, т.е. съотношението ъгъл допирателна:
Сега имаме всичко, което е необходимо, за да замести в горния влизането теоретична сертификат за да се получи уравнението на допирателната. получавам
В този пример, имахме късмет: Установено е наклонът е равен на нула, така че уравнението е отделно да доведе до общия външен вид не е необходимо. Сега можем да направим нормалното уравнение:
По-долу: график бордо функция тангента зелено, оранжево нормално.
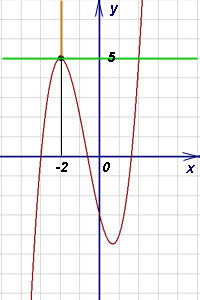
Следващият пример - не е трудно: функцията, както в предишния, който също е полином, но ъгловият коефициент няма да бъде нула, така че добавете още една стъпка - да донесе на уравнението на общата форма.
Пример 2. Създаване на уравнението на допирателната и нормално уравнението на графиката на функцията ако абсцисата на точката на допиране.
Решение. Намери ордината допирна точка:
Нека да намерите производната на функцията:
Намираме стойността на производното в точката на контакт, т.е. съотношението ъгъл допирателна:
Заместващ всички данни в "формула диска" и получаване на уравнението на допирателната:
Уравненията от общ изглед (всички букви и цифри, различни от нула, се събират от лявата страна и резерва дясната нула):
Се равнява на нормалното:
Пример 3. Създаване на уравнението на допирателната и нормално уравнението на графиката на функцията ако абсцисата на точката на допиране.
Решение. Намери ордината допирна точка:
Нека да намерите производната на функцията:
Намираме стойността на производното в точката на контакт, т.е. съотношението ъгъл допирателна:
Намираме уравнението на допирателната:
Преди да се намали на уравнението на общ ума нужда от него малко "четка": умножете срок от срок от 4. Правейки това води до уравнението на общата форма:
Се равнява на нормалното:
Пример 4. Създаване на уравнението на допирателната и нормално уравнението на графиката на функцията ако абсцисата на точката на допиране.
Решение. Намери ордината допирна точка:
Нека да намерите производната на функцията:
Намираме стойността на производното в точката на контакт, т.е. съотношението ъгъл допирателна:
Ние се получи уравнението на допирателната:
Тук е уравнението за общия вид:
Се равнява на нормалното:
Често срещана грешка при изготвянето на уравненията на допирателната и нормално - не видях, че функцията, в този пример - една сложна и изчисли нейната производна като производната на прости функции. Следващите примери - вече със сложни функции (съответстващи урок се отваря в нов прозорец).
Пример 5. Създаване на уравнението на допирателната и нормално уравнението на графиката на функцията ако абсцисата на точката на допиране.
Решение. Намери ордината допирна точка:
Внимание! Тази функция - сложна, тъй като аргументът на допирателната (2х) самата функция е. Следователно, ние откриваме, производното на функция като производно на съставна функция:
Намираме стойността на производното в точката на контакт, т.е. съотношението ъгъл допирателна:
Ние се получи уравнението на допирателната:
Тук е уравнението за общия вид:
Се равнява на нормалното:
Пример 6. Създаване на уравнението на допирателната и нормално уравнението на графиката на функцията ако абсцисата на точката на допиране.
Решение. Намери ордината допирна точка:
Както и в предишния пример, тази функция - е сложно, тъй като степента на () самата функция е. Следователно, ние откриваме, производното на функция като производно на съставна функция:
Намираме стойността на производното в точката на контакт, т.е. съотношението ъгъл допирателна:
Ние се получи уравнението на допирателната:
Тук е уравнението за общия вид:
Се равнява на нормалното: