Степента на площ от подобни триъгълници

Урок 17. геометрия 8 клас

В този урок ние ще формулира и докаже теоремата за отношението на областите на два подобни триъгълници. И реши някои проблеми. И в работата си с един от тях установихме, че съотношението на периметъра на два подобни триъгълници, равен на коефициента на сходство.

Кратък обзор урок "съотношение площ от подобни триъгълници"

В последния урок говорихме за да ви харесва, че се наричат ​​триъгълници, чиито ъгли са равни, и еднакви страни са пропорционални.

Броят на К, равен на съотношението еднакви страни на подобни триъгълници, наречен коефициента на сходство.

Припомнете си, че сходството на триъгълника е показан, както следва.

В този урок ще се докаже теоремата за отношението на областите на два подобни триъгълници.

Теорема. Съотношението на областите на два подобни триъгълници приликата коефициент, равен на квадрата.

, .

, .

, ,

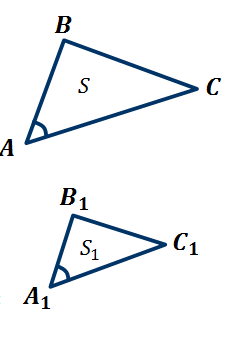
QED.

Задача. Площад на подобни триъгълници и равно на 2 см и 2 см см партия. Намери подходящо за да я страна на триъгълника.

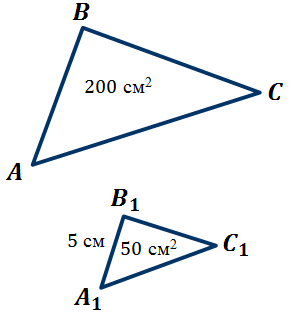
Над сме доказали, че отношението на областите на два подобни триъгълници е равен на квадрата на коефициента на сходство. ,,.

Задача. Докаже, че съотношението на периметъра на два подобни триъгълници равен на коефициента на сходство.

, , , , , .

, .

, ,

.

QED.

Задача. Триъгълници и са сходни. Еднакви страни и са равни на м см. Намерете отношението на периметрите на триъгълници и.

.

.

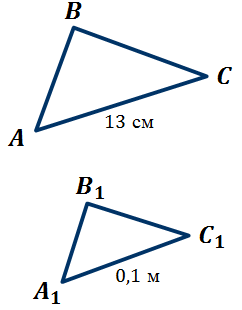
Така че, в този урок, сме доказали, че отношението на областите на два подобни триъгълници е равен на квадрата на коефициента на сходство. И ние решихме няколко проблема. И в работата си с един от тях установихме, че съотношението на периметъра на два подобни триъгълници, равен на коефициента на сходство.