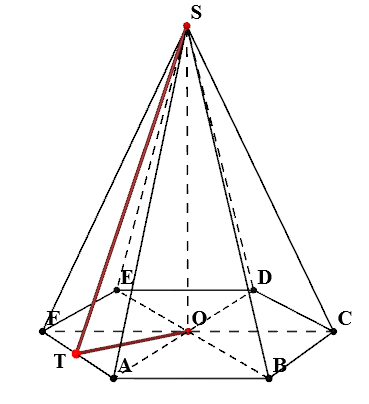
Редовен шестоъгълна пирамида Bank CSE

Редовен шестоъгълна пирамида - пирамида, чиято основа е правилен шестоъгълник.

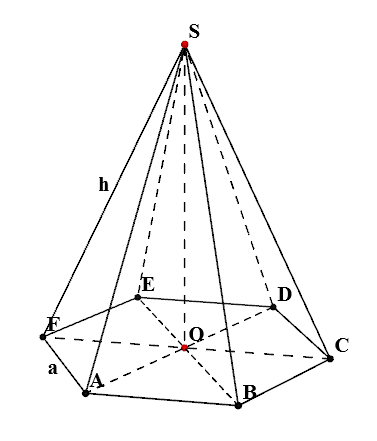
наименования

• $ SABCDEF $ - редовен шестоъгълна пирамида
• $ O $ - център основа на пирамидата
• $ A $ - дължина на страната на основата пирамида
• $ Н $ - дължината на страничните ръбове на пирамидата
• $ S _> $ - квадратна основа на пирамидата
• $ V _> $ - обем на пирамидата

Площта на база пирамида

В основата на пирамидата е правилен шестоъгълник със страна долара на $. Според свойствата на правилен шестоъгълник, квадратна основа на пирамидата е равна на S $$ _> = \ Frac> \ cdot на ^ 2 $$

Правилен шестоъгълник в дъното на пирамидата

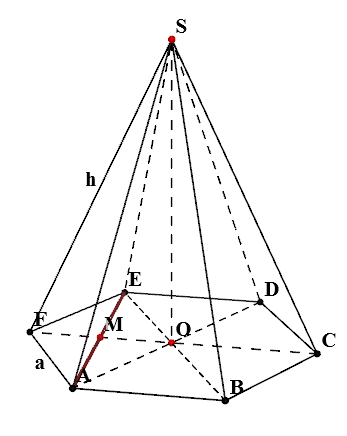
Според свойствата на правилен шестоъгълник, триъгълници AOB, BOC, COD, DOE, EOF, FOA са правоъгълен триъгълник. От това следва, че $$ AO = OD = ЕО = OB = СО = НА = а $$ нарязани тел на AE, пресича с CF сегмента на М. ОИО триъгълник равнобедрен, има $ AO = OE = а, \ \ ъгъл EOA = 120 $ ^. Според свойствата на равнобедрен триъгълник $$ AE = а \ cdot \ SQRT = \ SQRT \ cdot на $$ По същия начин можем да заключим, че $ AC = CE = \ SQRT \ cdot от $, $ FM = MO = \ Фрак \ cdot на $.

Намери $ $ на SO

Директно на SO $ $ е височината на пирамидата, така че $ \ ъгъл SOF = 90 ^ $. SOF триъгълник $ $ правоъгълен, в него $ FO = а, \ FS = Н $. Според свойствата на правоъгълен триъгълник $$ SO = \ SQRT = \ SQRT $$

Обемът на пирамидата

Обемът на пирамидата се изчислява като една трета от площта на основата на продуктите на височината му. Ръст на редовен пирамида се реже $ SO $. В основата на редовен шестоъгълна призма е правилен шестоъгълник, район, известен с нас. Получаване $$ V _> = \ Frac \ cdot S _> \ cdot SO = \ Frac> \ cdot на ^ 2 \ cdot \ SQRT $$

ST намерите $ $ $ и до $

Нека точка $ T $ е средната точка на $ ребрата $ AF. Триъгълник $ $ AOF коригира следователно свойствата на равностранен триъгълник $$ ДО = \ Фрак> \ cdot на $$ триъгълник на STO $ $ правоъгълен, височината на SO $ $ е $ \ SQRT $. По теоремата на Питагор $$ ST = \ SQRT = \ SQRT \ cdot на ^ 2> $$