методи прожекционни

За да се покаже оригиналната точка в чертежа се използва операция проекция. Налице е проекция равнина (понякога се нарича картина равнина), в която се получава оригиналното изображение - проекцията на точка А. операция се състои в извършване през точка А на правата линия, която се нарича проектиране.

А1 точка - точката на пресичане на равнината на издаващия права P1- наречен проекцията на точка А на равнина Р1.

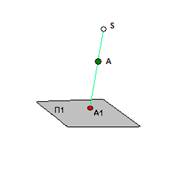
Чертежи, конструирани чрез метода на проекция се нарича проекция.

В зависимост от позицията на проекция на издадените лъчи може да бъде или централната (коничната) или паралелно (цилиндрична).

При проектиране на комплекс обект се очаква всяка точка.

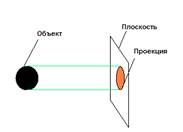
Най-честият случай на получаване на прогнози пространствени фигури - е централната издатина.

В този случай, издадените греди, излизащи от една точка - прогнозния центъра S, която е на разстояние от ограничен проекция равнина Р1.

За да се получи централната проекцията на точки А и В трябва да извърши проектиране лъчи от проекция центъра на S чрез точки А и В на пресичане Р1 с проекция равнина. Когато пресечните точки се получават А1 и В1 - централната проекцията на точки А и В.

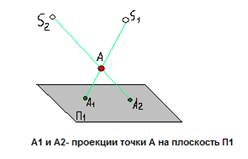
Позицията на точка S и равнина Р1. който не преминава през центъра на проекция, централното звено определя проекцията. Ако е настроен, тогава ние винаги може да се определи позицията на всяка точка на централната проекция пространство на проекционната равнина, където всяка точка в пространството, ще има само една централна проекция. Въпреки това, един от централния проекцията е невъзможно да се определи местоположението на точка в пространството, тъй като тя може да е навсякъде в линията, свързваща проекцията на точката и центъра на проекция.

За да се определи позицията на точка А в пространството на централната издатина трябва да има два централни проекции на този етап А1 и А2 са получени от две различни точки S1 и S2. Ако теглим лъчите стърчащи S1A1 и S2A2, тяхната пресечна точка недвусмислено определяне на позицията на точка А в пространството.

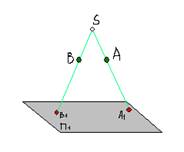
За конструиране на централната издатина A1B1 сегмента AB е достатъчно за изграждане на централните издатини А1 и В1 точки А и В, тъй като двете точки еднозначно определят права линия.

прогнози цени на имотите в центъра на проекцията:

1 е проекция на точка точка.

2 проекция на линията е ред.

3 Проекцията на права линия обикновено е права линия. (Ако линия съвпада с издаващия лъч, неговата издатина е точката).

4 Ако точката принадлежи към линията, проекцията на точката принадлежи на проекция линия.

5 линии на пресичане точка се очаква до точката на пресичане на проекциите на тези линии.

6 общо плоска многостен очаква многостен със същия брой върхове.

Проекцията 7 от взаимно успоредни линии е молив линии.

8 Ако равнина фигура е успоредна на равнината проекция, неговата издатина е подобен на фигурата.

Паралелно проекция може да се разглежда като специален случай на централно проектиране.

Ако центърът на проекцията в централния офис на проекцията да бъдат преместени до безкрайност, а след това проектиране лъчите може да се разглежда паралелно. Следователно, апаратът се състои от паралелно проекция равнина на прожекционни посоки Р и R. Когато централните прожекционни стърчащата лъчи излизат от една точка, и стърчащи паралелен - паралелно.

В зависимост от посоката на проектиране паралелно проекция лъч може да бъде наклонена. когато стърчащата греди са наклонени спрямо равнината на проектиране, и правоъгълна (ортогонална). когато стърчащи лъчи са перпендикулярни на равнината на проектиране.

Построява паралелно проекция A1B1 сегмент AB на равнина Р1 в предварително определена посока проекция Р е Р1. Това изисква проектиране прави линии през точките А и В, успоредна на проекцията P. При преминаване стърчащата направо от Р1 равнина издатини паралелни се получават А1 и В1 точки А и В са свързани паралелно проекция на А1 и В1, ние получаваме успоредна проекция на A1B1 сегмент AB.

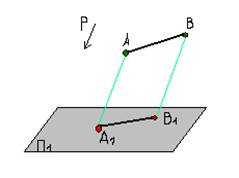
По същия начин, може да се изгради паралелно проекция A1V1S1D1 четириъгълник ABCD на равнина Р1 в предварително определена посока проекция Р е Р1.

Това изисква проектиране линии чрез точки А, В, С, D, успоредна на R. посока Когато се получават проекцията стърчащата линии, пресичащи с издатини равнина Р1 паралелни А1, В1, С1, D1 точки А, В, С, D. Комбинирането паралелни проекции А1, В1, С1, D1 ние получаваме успоредна проекция A1V1S1D1 четириъгълник ABCD.

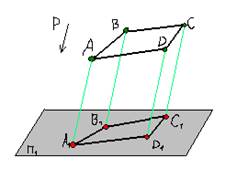
Свойства на проекции в паралел:

1.Proektsii успоредни линии паралелно.

Тя може да се види, че линии AA1, BB1, CC1 и DD1 образуват две успоредни равнини, а и б. Тези две равнини се пресичат с Р1. Следователно, линията на пресичане на A1B1 и S1D1 са успоредни.

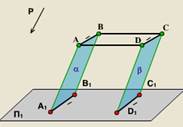
2. Ако точката разделя дължината на сегмента по отношение на m: п, след проекцията на тази точка разделя дължината на проекцията на сегмента на същата основа.

Нека точка С принадлежи към сегмента AB, а | AC |. | CB | = 1. 2. Да се ​​изгради паралелна проекция на отсечката A1B1 AB. Точка C1 A1B1. Начертайте AC '|| A1C1 и ТБ "|| C1B1, получаваме две подобни триъгълници ACC "и СВВ". Приликата им трябва да бъде пропорционално на страните: | AC |. | CB | = | AC '|. | CB '|, но | CB' | = | S1V1 | и | AC '| = | A1C1 |, следователно | AC |. | CB | = | A1C1 |. | C1B1 |.

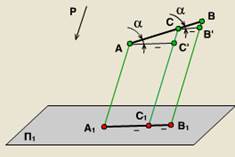
3. плоска форма успоредно на равнината на проекция се очаква без изкривяване.

Вземете триъгълника ABC и го прожектирате две паралелни равнини на Р1 прогнози "и Р1. Тъй като сегменти на дължина, равна на | A1 A1 '| = | B1 B1 '| = | C1 C1 '| и сегменти са паралелни, четириъгълници А1 А1 "В1, В1", В1, В1 "S1S1", С1 S1'A1A1 "са паралелограми. Следователно, срещуположните страни на еднаква дължина | А1 В1 | = | А1 "В1" |, | В1, С1 | = | В1 "С1" |, | А1 С1 | = | А1 "С1" |, което означава, че триъгълници са равни.

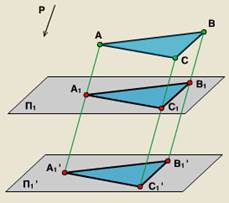
По същия начин, същото може да се докаже за други плоски форми. Паралелно проекция, за разлика от централната притежава по-малко яснота, но осигурява много проста конструкция и връзката на оригинала.

Както бе споменато по-горе правоъгълната проекция - специален случай на паралелно проекция. В ортогонална проекция стърчащи лъчи са перпендикулярни на равнината на проектиране.

Апаратът на издатината се състои от една равнина на проекция.

За получаване на ортогонална проекция на точка А до е необходимо да се държи стърчащата лъч перпендикулярна Р1. А1 точка се нарича ортогонална или правоъгълна проекция на точка А.

За да ортогонална проекция на A1B1 сегмент AB на равнина Р1, е необходимо чрез точки А и В да държи стърчащата прави линии Р1. При преминаване издадените линии се получават с равнина Р1 издатини ортогонални А1 и В1 точки А и В. Чрез комбиниране на проекции А1 и В1 получат ортогонална проекция A1B1 сегмент AB.

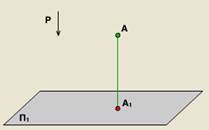
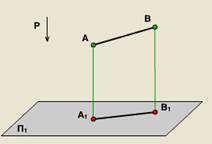
Всички свойства на успоредна проекция възможно и ортогонална проекция. Въпреки това, проекции имат още няколко свойства.

Свойства на правоъгълната проекция на:

дължина 1.Dlina равна на дължината на нейната издатина, разделен на косинуса на ъгъла на наклон на сегмента на проекция равнина.

Вземете линия AB и изграждане си ортогонална проекция на Р1 равнина A1B1. Ако начертаете права линия AS || A1B1, а след това на триъгълника ABC, то следва, че | AC |. | AB | = Cos а и | AB | = | A1B1 |. защото един, т да | .. A1B1 | = | AC |.

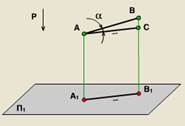
2. В допълнение, за ортогонална проекция теоремата е за проектиране на десния ъгъл:

Теорема: Ако най-малко едната страна на десния ъгъл е успоредна на равнината на проекция, а вторият не е перпендикулярна, ъгълът на тази плоскост се очаква в пълен размер.

Доказателство: Дан прав ъгъл ABC, който от хипотеза, линията BC AB и BC || Р1 проекция равнина. Чрез изграждането на директна линия на слънцето се очаква да BB1. Следователно, пряка слънчева към равнина б (AVhVV1) т. К. две пресичащи се линии. лежи в равнината. От условието за пряко B1C1 || Слънцето, така също и за самолет б, че. Д. и линия A1B1 прав, че самолет. Следователно, ъгълът между правите линии и A1B1 B1C1 е 90 °, както се изисква.

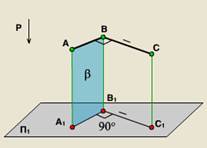
Правоъгълната проекция геометрични конструкции осигурява лесното определяне проекции на точките, както и способността за съхранение на проекциите на формата и размерите на проектираното фигурата. Тези предимства са предоставили ортогонална проекция широко използван в техническия чертеж.

Горните проекционни методи могат да решат проблема директно на описателен геометрия, т. Е. След първоначалното изграждане на плосък чертеж. Получените по този начин издатините на един самолет дава непълна картина на обекта, си форма и положение в пространството, т.е.. Е. Няма такъв чертеж има свойството на обратимост.

За да се получи обратимо рисунка, т.е. изготвяне дава пълна картина на формата, размера и позицията на оригинала в пространството, привличайки odnokartinny допълнение. В зависимост от добавките, има различни видове рисунки.

1.Epyur Monge или ортогонална проекция.

метод ортогонална (правоъгълна) проекция е, че оригинала ортогонално проектирана върху два или три взаимно ортогонални равнина на проекция и след това да ги комбинира с равнината на чертежа.

аксонометрични същността рисуване, че първият оригинала е здраво свързан с декартова координатна система OXYZ, ортогонално проектиране на един от своите самолети на проекция OXY, или OXZ. След това, успоредна проекция са успоредни на проекцията на Полученият конструкт: OX оси, OY, OZ, на вторичните издатини и оригинала.

При изграждането на перспектива сграда изготвяне първо една ортогонална проекция, а след това в самолета на централната проекция са изградени по-рано и е правоъгълната проекция на оригинала.

4.Proektsii с цифрови означения и др ..

За да се получи проекция с цифрови означения се очаква перпендикулярно на първоначалното ниво нула равнина и точка от първоначалната точка на равнината.