Кинематика на материална точка

Основни материали точка кинематика с формула

Представяме основната формула кинематика материал точка. След това ние даваме своя деривация и обсъждане на теорията.

вектор радиус на материална точка М в правоъгълна координатна система Oxyz:






,
при което - вектори единица (вектори) в посока на осите X, Y, Z.

скорост точка:
;
.
.
вектор елемент в посока допирателната към траекторията на:
.

Тангенциална (срязване) Ускорение:
;
;
.

Единичен вектор насочени към центъра на кривината на траекторията на точка (по протежение на основната нормалата):
.

Радиусът на кривата на траекторията:
.

Следното е получаване на тези формули и описанието на теорията на материална точка кинематиката.

Векторът на радиус и траекторията на точката

Разглеждане на движението на материала точка М. Ние избере фиксирана правоъгълна система в някои фиксирана точка О. Oxyz координира с позицията център на точката М след това еднозначно определена от нейните координати (х, у, Z). Тези координати са компонентите на радиус вектор от материал точка.

вектор радиус на точка М - е вектор. съставен от фиксиран система на координати на точката О М.
,
при което - вектори единица по осите X, Y, Z.

Когато движението на точка с координати се променят с времето. Тоест, те са функции на времето. Тогава системата уравнения
(1)
Тя може да се разглежда като уравнение на кривата, определена от параметрични уравнения. Такава крива е траекторията на една точка.

Траекторията на материална точка - това е линията, по която движението на точката на случва.

Ако вотът на точка в равнината, можете да изберете оста и координатната система по такъв начин, че те лежат в равнината. Тогава траекторията се определя от двете уравнения

В някои случаи тези уравнения могат да елиминират времето. Тогава уравнението на траекторията ще има връзка на формата:
.
където - функция. Тази зависимост е само с променливи и. Тя не съдържа параметър.

Скоростта на материал точка

Speed ​​материална точка - това е производно на вектора на радиус по отношение на времето.

По дефиниция, скорост и определение на производното:

Производните по отношение на времето, в механика, означават точка горе символ. Ние замени изразът за вектор радиус:
.
където ние ясно идентифицирани зависимостта на координатите на време. получаваме:

- скорост проекция на оста на координатната. Те се получават по време диференциране радиус вектор компонент
.

по този начин
.
единица скорост:
.

В допирателната към траекторията

От математическа гледна точка, системата от уравнения (1) може да се разглежда като уравнение на линия (крива), определена от параметрични уравнения. Time. В такъв анализ, той играе ролята на параметър. Разбира се на математически анализ е известно, че в посока вектор на допирателната към тази крива има следните компоненти:
.
Но това е компонент на вектора на скоростта на точката. Това е скоростта на материалната точка е допирателна към траекторията.

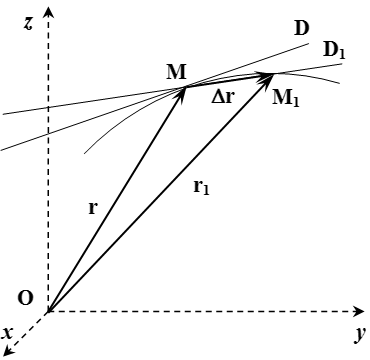
В допирателната към траекторията на точката

Всичко това може да се демонстрира директно. Да предположим, че по време на точка съхранява в позицията на вектора на радиус (вж. Фигура). И в момента - в позицията на вектора на радиус. Чрез точките и да начертаете линия. По дефиниция, допирателната - това е една линия. Целта й е прав в.
Представяме нотация:
;
;
.
Тогава векторът е насочен по продължение на линията.

В аспирация. Директен клони към допирателната. и вектора - на скоростта на точката във времето.
.
Тъй като вектор е насочен по продължение на линията. и по отношение на всяко. вектора на скоростта се отнася по допирателната.
Това означава, че векторът скорост на точката на материал е насочено по допирателната към траекторията.

Ние въведе посока допирателна вектора на единица дължина:
.
Ние показваме, че дължината на този вектор е равен на единица. В действителност, тъй
. след това:
.

Тогава вектора скорост на точката може да се представи като:
.

Освен това, ние вярваме, че ако писмото от количеството на вектор не е стрела, това означава единица вектор.

Ускорението на материалната точка

Ускоряване на материална точка - това е производно по отношение на скорост време.

Подобно на по-горе, ние получаваме ускорение компоненти (ускорение проекция на координатните оси):
;
;
;
.
ускорение модул:
.

Тангенциална (допирателна) и нормалното ускорение

Сега да разгледаме въпроса за посоката на вектора на ускорението по отношение на траекторията. Към това можем прилага формулата:
.
Ние го диференцират във времето, прилагането на правилото за диференциране на продукта:
.

Вектор е насочено по допирателната към траекторията. В каква посока насочено негово производно по отношение на времето.

За да отговорим на този въпрос, ние използваме факта, че дължината на вектора е постоянна и равна на единство. Тогава квадрата на дължината му е равна на единство:
.
Тук и по-долу, два вектора в скоби означават скаларен продукт на вектори. Разграничаваме това уравнение по отношение на времето:
;
;
.
Тъй като точка продукта от два вектора и е равна на нула, тогава векторите са перпендикулярни една на друга. Тъй като векторът е насочено по допирателната към пътя, след това векторът е перпендикулярно на допирателната.

Първият компонент по-долу тангенциална или тангенциално ускорение:
.
Вторият компонент се нарича нормално ускорение:
.
Тогава общото ускорение:
(2).
Тази формула представлява ускорение разлагане в две взаимно перпендикулярни компоненти - допирателната към траекторията и перпендикулярно на допирателната.

Тангенциална (допирателна) Ускорение

Увеличаването двете страни на уравнение (2) на скаларен продукт.
.
Тъй като. след това. след това
;
.
Тук ние поставяме:
.
Това показва, че тангенциално ускорение, равно на ускоряване на пълното проекция на посоката на допирателната към траекторията, или, еквивалентно, посоката на скоростта на точката.

Тангенциална (допирателна) ускоряване на материал точка - това е проекция на пълния ускорение в посока допирателната към траекторията (или посоката на скоростта) на.

Символ ще означаваме вектор тангенциално ускорение насочени по допирателна към траекторията. След това - това е скаларно количество, равно на проекцията на общото ускорение в посока на допирателната. Тя може да бъде положителен или отрицателен.

Заместител при формула:
.
След това:
.
Това е тангенциално ускорение е време производно на модула на точката на скорост. По този начин, тангенциално ускорение предизвиква промяна в абсолютната стойност на температурата на скорост. С увеличаване на скоростта, тангенциалната ускорение е положителен (или насочени по протежение на скоростта). При намаляване на скоростта на тангенциален ускорение е отрицателен (или обратната насочено скоростта).

Радиусът на кривата на траекторията

Сега ще разгледаме вектора.

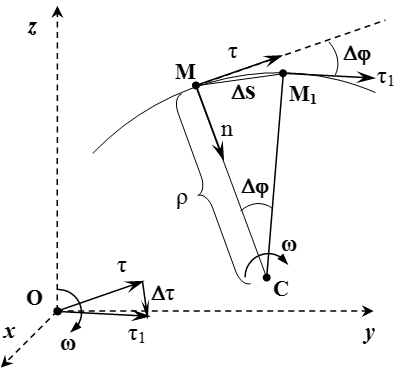
Радиусът на кривата на траекторията

Помислете за единица вектор допирателната към траекторията на. Сложете го обратно към произхода на координатната система. След края на вектора ще бъде сфера единица. Когато движението на частиците, в края на вектора ще се движат през този район. Това означава, че ще се завърти около произхода му. Да - моментната ъглова вектора скорост в даден момент. След неговото производно - е скоростта на края на вектора. Е перпендикулярна на вектора. Ние прилагаме формулата за въртеливо движение. вектор модул:
.

А сега да разгледаме положението на точка в продължение на две близки моменти от време. Да предположим, че в момента се помещава точка. и в даден момент - в държавата. Нека - вектори единица насочени по допирателна към траекторията на тези точки. Чрез точките и изготвя равнина, перпендикулярна на векторите и. Да - права линия, образувана от пресичането на тези самолети. От гледна капка перпендикулярна на линията. Ако позициите на точките са достатъчно близки, движението на точката може да се разглежда като радиусът на въртене около обиколката на ос. което ще бъде мигновен оста на въртене на материал точка. Тъй като вектори и са перпендикулярни на равнините и. ъгълът между две равнини, равен на ъгъла между векторите и. Тогава моментната скорост на въртене на точка около оста на въртене е равна на вектора на моментната скорост.
.
Ето - разстоянието между точките и.

Така че ние открихме модул производно вектор от време.
.
Както вече беше посочено, вектор, перпендикулярна на вектора. От горната дискусия е ясно, че то е насочено към пътя на моментния център на кривината. Тази посока се нарича основната нормалното.

нормално ускорение

насочена по вектора. Както видяхме, този вектор е перпендикулярна на допирателната към страната на моментния център на кривината на траекторията.
Нека - единица вектор насочено от материал, точка на моментния център на кривината на пътя (по протежение на основната нормален). след това
;
.
Тъй като и двете вектор и да имат една и съща посока - към центъра на кривината на траекторията,
.

От формула (2), имаме:
(4).
От формула (3) намираме нормална модул ускорение:
.

Увеличаването двете страни на уравнение (2) на скаларен продукт.
(2).
.
Тъй като. след това. след това
;
.
Това показва, че нормалната модула ускорение е проекция на общия ускорение в посоката на главния нормалното.

Нормално ускорение на материална точка - проекция на пълния си ускорение от посоката, перпендикулярна на допирателната на път.

Ние замени. след това
.
Това означава, че ускорението води до промяна в посока на точката на скорост и тя е свързана с радиус на кривината на траекторията.

От тук можете да намерите радиусът на кривината на траекторията:
.

В заключение, ние се отбележи, че с формула (4) може да бъде пренаписана в следната форма:
.
Тук се прилага формулата за кръстосано продукт на основните елементи:
.
който е в рамка
.

По този начин, ние имаме:
;
.
Ние приравняваме модули лявата и дясната страна:
.
Но вектори и са взаимно перпендикулярни. следователно
.
след това
.
Известно е от диференциалната геометрия формула за кривината на кривата.