Какво е ковариацията
Характерна връзка между случайни величини х и у е очакването работи х и у отклонения на центровете на техните разпределения (понякога по-нататък математическото очакване на случайна променлива) се нарича коефициент на ковариация или просто ковариация.
Тази формула може да се тълкува, както следва. Ако за големи стойности на х е по-вероятно по-големи стойности на Y, и при малки стойности на X са по-склонни малки стойности Y, а след това от дясната страна на ковариацията положителна доминират и ковариацията отнема положителни стойности.
Ако по-вероятно продукт (XI - EX) (YJ - EY), състоящ се от факторите на противоположни знаци, т.е. изхода на случаен експеримент води до големи стойности на X обикновено води до малки стойности на Y и обратно, ковариация получава голям абсолютен отрицателен стойности.
В първия случай е прието да се говори за директна комуникация: като случайна променлива X Y има тенденция да се увеличават.
Във втория случай говорим за обратна връзка: като X случайна променлива Y има тенденция да намалява или да падне.
Ако приблизително същото принос в размер на добив и двете положителни и отрицателни продукт (XI - EX) (YJ - EY) PIJ. можем да кажем, че заедно могат да "гасят" помежду си, а ковариацията ще е близка до нула. В този случай, не се вижда зависимостта на случайна променлива на другия.
Лесно е да се покаже, че ако
Наистина, от (2)
Тук сме използвали много важно свойство на очакването: очакване на случайна променлива отклонения от неговото математическо очакване е равно на нула.
Ковариация удобно представени под формата на
Ковариацията на две случайни величини е равна на очакването на техния продукт минус продукт на очакванията.
Както за независими променливи EXY = EXEY, очевидно е, че за независими случайни променливи X и Y CoV (X, Y) = 0.
Определение. На случайни величини, ковариацията е нула, наречени на несвързани помежду си.
.Забележка. Както е показано по-горе, от независимостта на случайни величини да бъдат тях несвързани помежду си, която е равна на нула корелация. Обратното не е вярно! Помислете за подходящ пример:
Нека случайна променлива X има равномерно разпределение на интервала (1, 1) и случайна променлива Y е свързан с случайна променлива X функционална връзка Y = X 2. Ние показваме, че CoV (X, Y) = 0, въпреки че има функционална връзка.
Като се има предвид. че EX = 0 (в средата на интервала (-1,1)), получаваме:
CoV (X, Y) = EXY-EXEY = EX = 3
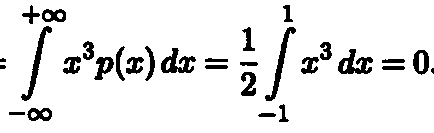
Така че, на несвързани помежду си случайни величини не трябва да бъде тяхната независимост.
Ковариация случайни стойности отразяват степента на зависимост на случаен близост променливи до линейни, т.е. зависимост от формата Y = AX + B.
Да разгледаме сега друга мярка на линейна зависимост - коефициент на корелация на случайни променливи X и Y R (х, у) =
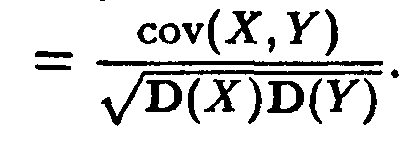
Може да възникне въпросът, защо се въведе още една мярка за линейна зависимост?
Корелационният коефициент варира от -1 до 1, вместо цялата реално оста
Коефициентът на корелация, за разлика от ковариацията нечувствителен към променящите единици
Ако случайни променливи са независими, коефициента на корелация като ковариацията е нула.
Ако случайна стойност е линейно зависим, тогава R = 1 - пряка връзка. г = -1, обратното. И обратно, за равенство модул 1 трябва да бъде линейна зависимост.
Нека разпределението на случайни променливи е посочена таблица
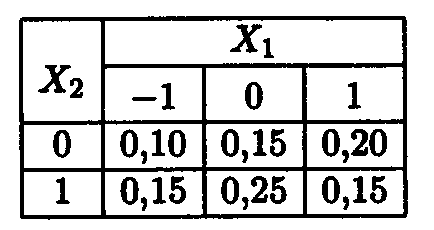
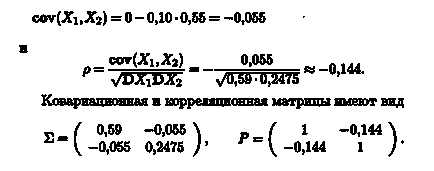
Забележка. Ковариация и корелация матрица - маса, съответно, на коефициентите на ковариация и корелационните съответните случайни променливи. (Забележете, че основната диагонала на матрицата на корелация са 1 - случайна променлива, очевидно със себе си е линейна функция). Използвайте тези матрици за визуализиране на връзката на стойности на данни и статистика.