Как да си намерим диагонал площ на напречното сечение

Диагоналът на куб сечение има формата на правоъгълник, чиято площ (S) е лесно да се изчисли, знаейки, дължината на всяко ребро (а) в насипно състояние. Този правоъгълник на една от страните ще бъде на височината на която съвпада с дължина на ръба. Дължината на друга - диагонал - изчислителната от Питагоровата теорема за триъгълник, в които е хипотенузата и двата края на основата - краката. В общи линии, това може да се запише като: * √2. Площта на диагоналната част намерете размножаването на двете си страни, дължината на които сте намерили: S = а * а * √2 = ² * √2. Например, когато дължината ръб 20 см диагонал сечение на куба трябва да бъде приблизително 20² * √2 ≈ 565 686 cm².

За да се изчисли сечение напречно на диагонала на паралелепипед (S) се процедира по същия начин, но се отбележи, че в Питагоровата теорема в този случай включва краката на различна дължина - дължина (L) и фигури ширина (W) на звука. Дължина на диагонала в този случай ще бъде равна на √ (l² + w²). Височината (Н) може също да се различава от дължината на ръбовете на основи, така че в обща формула сечение може да се изписва като: S = Н * √ (l² + w²). Например, ако дължината, височината и ширината на паралелепипеда, са съответно 10, 20 и 30 cm, неговата диагонал сечение е приблизително 30 * √ (10² + 20²) = 30 * √500 ≈ 670,82 cm².

диагонален разрез четириъгълна пирамида има триъгълна форма. Ако височината (Н) на многостен е известен, и в основата си се състои правоъгълник, дължината на съседните ръбове (А и В), които са в същите условия, изчисляване на площта на напречното сечение (S) се започне с изчисляване на диагонала на основата. Както и в предходните стъпки за използване на двата края на триъгълника и основата диагонал където Питагоровата дължина на хипотенузата е равна √ (² + b²). Височината на пирамидите в полихедронов съвпада с височината на триъгълника на диагоналната част. спуска към страната, дължината на която току-що сте дефинирани. Ето защо, за намиране на площта на триъгълник получите височината половината от продукта по дължината на диагонала: S = ½ * H * √ (² + b²). Например, на височина 30 cm и дължина на съседни страни на основата 40 и 50 cm диагонал сечение трябва да бъде приблизително равна на ½ * 30 * √ (40² + 50²) = 15 * √4100 ≈ 960,47 cm².

Изчислете необходимата дължина. Използване обща формула: пирамида дължина ръб равно корен сума от квадратите на разликите в съответните координати на граничните точки. Заместник номера координатите си във формулата и да намерят дължината на ръбовете на пирамидата. По същия начин се дължината на ребрата не само редовен пирамида. но правоъгълна и пресечен и произволно.

Да се ​​намери дължината на ребрата на пирамидата. всички от чиито ръбове са равни, цифрите, определени база страна и известна височина. Определя височина местоположение на основа, т.е. долната си точка. Тъй като ребрата са еднакви, така че е възможно да се направи кръг, който е пресечната точка на диагоналите на центъра на основата.

Начертайте права линия, свързваща противоположните краища на основата на пирамидата. Маркирайте точката, където те се пресичат. В една и съща точка и ще бъде по-ниска граница на височината на пирамидата.

Да се ​​намери дължината на диагонала на правоъгълника с помощта на питагорова теорема, когато сборът от квадратите на краката на правоъгълен триъгълник е равен на квадрата на хипотенузата. Вземи a2 + b2 = c2, където А и Б - на краката, а с - хипотенузата. Тогава хипотенузата е равен на корен квадратен от сумата на квадратите на другите две страни.

Да се ​​намери дължината на ребрата на пирамидата. На първо място, се разделят на дължината на диагонала на половина. Всички получени стойности на данни за заместване в Питагоровата формула описано по-горе. Подобно на предишния пример се коренът на сумата от квадратите на височината и половината от дължината на диагонала на пирамидата.

• как да се намери дължината на ръба на координатите

Това се нарича аксиален разрез, който преминава през геометричната ос на тялото, образуван от въртенето на определена геометрична фигура. Цилиндърът получени чрез въртенето около една от страните на правоъгълник, а това са дължи на многобройните си свойства. Формиране тази геометрична тялото са успоредни и равни помежду си, което е много важно да се определят параметрите на своята осово сечение, включително по диагонал.

• - цилиндър с предварително определени параметри;
• - хартия;
• - молив;
• - линия;
• - на компасите;
• - Питагорова теорема;
• - теорема на Синиш и уют.

Построява цилиндър съгласно предварително определени условия. За да може това да се направи, трябва да знаете, радиусът на основата и височината. Въпреки това, други условия могат да бъдат определени в дефиницията за задача в диагонала - например, ъгълът между диагонала и образуваща или основа диаметър. В този случай, при създаване на чертеж, направен с размера, който сте задали. Останалата част се вземат произволно и посочи, че се дава на вас. Определяне точката на пресичане ос и бази като О и О '.

Начертайте аксиален. Това е правоъгълник, двете страни на които са диаметрите на основи и другите две - генераторите. Тъй като двете образуващи перпендикулярни основа и двете са височини на геометричната тялото. Определяне получената правоъгълника като ABCD. Прекарайте диагонал AC и BD. Не забравяйте свойствата на диагоналите на правоъгълника. Те са равни помежду си и да се раздели на две в пресечната точка.

Да разгледаме триъгълник ADC. Той е прав, защото CD-изображението е перпендикулярно на земята. Един крак е с диаметър от основата, а вторият - формиране. Диагоналът е хипотенузата. Помислете за това как да се изчисли дължината на всяка хипотенуза на правоъгълен триъгълник. Той е равен на корен квадратен от сумата на квадратите на другите две страни. Това означава, че в този случай г = √4r2 + h2, където г - диагонал, г - радиусът на основата, и Н - височина на цилиндъра.

Ако проблемът не се дава на височината на цилиндъра, но определен ъгъл секцията диагонал аксиален с основа или чрез използване на синус или косинус теорема. Спомнете си, че означава функциите тригонометричните данни. Това е връзката на обратното или съседни предварително определен ъгъл крака към хипотенузата на, че вие ​​и да се намери. Да предположим, че сте настроили височината и ъгъла между CAD и диагонала на база диаметър. В този случай, използвайте синусова теорема, тъй като ъгъл CAD е срещу образувателна. Откриване хипотенуза г от формула D = H / sinCAD. Ако сте задали радиуса и под същия ъгъл, използвайте теоремата за уют. В този случай, D = 2г / защото CAD.

По същият принцип се прилага в случаите, когато под определен ъгъл ACD между диагонала и генератора. В този случай, задължително теорема се използва, когато даден радиус и уют - ако знаете надморската височина.

Построява повърхност пресечната линия с пирамидална стърчащата предна равнина Σ (Σ2).
Първо маркирайте желаните точките на секции, които могат да бъдат определени без помощни равнини раздел.

Σ пресичат базовата равнина на пирамидата в права линия 1-2. Забележка точка 12≡22 - изглед отпред на тази права линия - и с помощта на вертикална връзка изградят свои хоризонтални проекции 11,21 на страни и основа A1C1 B1C1 на

Rib SA (S2A2) пресича равнината на пирамида сигма (Σ2) в точка 4 (42). хоризонтална проекция, използващи S1A1 ребра получите точка за връзка 41.

3 през точка (32) изпълнява като спомагателна рязане равнина ниво хоризонтална равнина T (Т2). Това е успоредна проекция равнина Р1 и разрез с повърхността на пирамида воля триъгълника на подобен на основата на пирамидата. На S1A1 E1 посочва моментът S1S1 - точка K1. Равен линии, успоредни на страните на пирамида база A1V1S1 и се S1V1 ръб точка 31. съединителни точки 11, 21, 41, 31, получават хоризонталната проекция на желания раздел повърхност пирамида предварително определена равнина. Предната част проекция съвпада с проекцията на предна равнина сигма (Σ2).

На S1A1 E1 посочва моментът S1S1 - точка K1. Равен линии, успоредни на страните на пирамида база A1V1S1 и се S1V1 ръб точка 31. съединителни точки 11, 21, 41, 31, получават хоризонталната проекция на желания раздел повърхност пирамида предварително определена равнина. Предната част проекция съвпада с проекцията на предна равнина сигма (Σ2).

Следователно, проблемът е решен, изхождайки от принципа открити по точки едновременно, принадлежащи към две геометрични елементи - повърхността на пирамида и предварително определена равнина рязане Σ (Σ2).

Опитайте с по-общ проблем да се анализират подробно изграждането на напречното сечение на куба.
Нека рязане равнина линията на пресичане на дефинирани собствена равнина и равнината, съдържаща долната основа на кутията L и ъгъла на равнината Р.
Цялата принципа на конструкция е илюстрирана на Фигура.

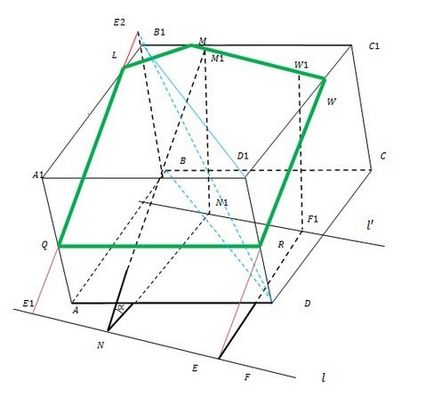
Решение.
Всеки ъгъл на геометрични проблеми на строителството не се определя от ъгъла, и никоя от нейните тригонометрични функции, то нека това бъде котангенс (CTG). Необходимо е да се измери във всяка метрична система разтвор дължина компаси Nctgf = г. Преместване на тази стойност в мащаба на проблема и, въз основа на принципа на подобието на правоъгълен триъгълник с общ малък ъгъл, направете следното.

L на линията вземат две произволни точки N и F (така че е желателно да бъдат по-нататък продължава в долната основа ABCD куба). От тях като център, начертайте радиус дъга г в ABCD. Тези дъги плъзват обща допирателна л до пресичането му с AB и CD (може да продължи). докоснете точка N1 марки и F1.

От N1 и F1 е необходимо да се повиши вертикалите М1 и W1 на горната основа A1B1C1D1, дължината на който е равен на Н. Следователно, точката на пресичане да изглежда не е необходимо, въпреки че е съвсем проста. Сега разшири M1W1 сегмент за подтискане с B1C1 и S1D1 в М и W съответно. Така че сте открили първата страна на желаната част MW.

След това, в рамките на равнината, съдържаща странична повърхност DCC1D1, направи линия от точка WE W (Е - неговото пресичане с права линия L). Ние пресичане с D1D - точка R. Cut WR - втори край на желаната секция.

Разширяване ВВ1 страничен ръб на куба в посока от В до В1. Диагоналната равнина на куб сечение BB1D1D R Прекарайте линия до неговото пресичане с ВВ1 разширение в точка Е2. От тази ниска линия до неговото пресичане с л Е1. Директен E1E2 пресича на страничните ръбове на куб и A1B1 AA1 на в точки L и Q, съответно. Тогава ML, LQ и QR - остава желания ребро раздел на куба.

В много учебници намерили работа, свързани с изграждането на участъци от различни геометрични фигури, включително кутията. За да се справи с тази задача, тя трябва да бъде въоръжен с известни познания.