Как да направите графика на квадратно уравнение

Графиката на квадратното уравнение на формуляра ос 2 + BX + C или (х - з) 2 + к е парабола (U-образна крива). За парцел това уравнение е необходимо да се намери в горната част на параболата, посоката и точката на пресичане с оси X и Y. на Ако са дадени относително прост квадратно уравнение, може да замести различните стойности на "х", намери съответната стойност на "Y" и изготвя графика ,

стъпки Редактиране

За парцел трябва да намери числовите стойности на коефициентите A, B, C (или, з, к). По-голямата част от проблемите са квадратно уравнение с числовите стойности на коефициентите.

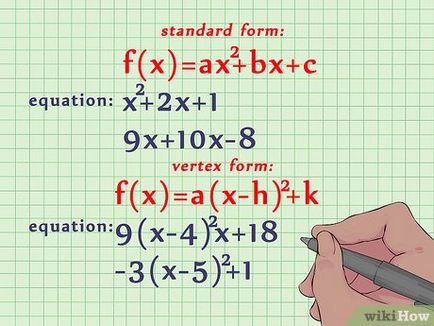
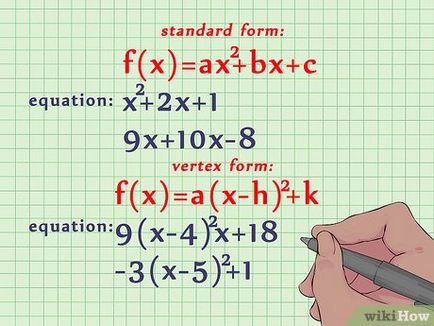
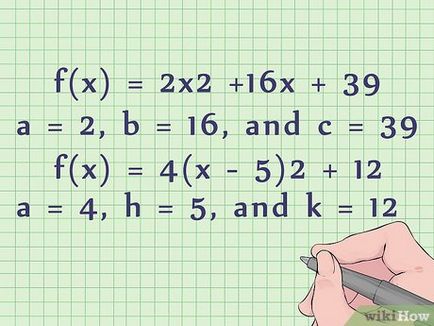
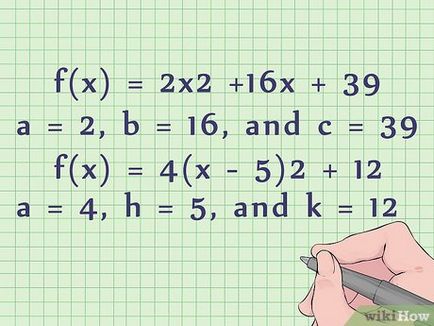
• Например, в стандартната уравнение е (х) = 2 х 2 + 16x + 39 а = 2, б = 16, с = 39.
• Например, в нестандартно уравнение е (х) = 4 (х - 5) 12 + 2, а = 4, з = 5, к = 12.

Изчислява час в стандартен уравнение (в нестандартно, тя вече е дадено) с формулата: з = Ь / 2а.

• В нашия пример, стандартната уравнение е (х) = 2 х 2 + 16x + 39 Н = Ь / 2а = -16 / 2 (2) = -4.
• В този пример, обичай уравнение е (х) = 4 (х - 5) 12 2 + Н = 5.

Изчислете стандартната уравнение к (вече дадени в това нестандартно). Имайте предвид, че к = F (з), което означава, можете да намерите к, замествайки в първоначалното уравнение получената стойност з вместо "х".

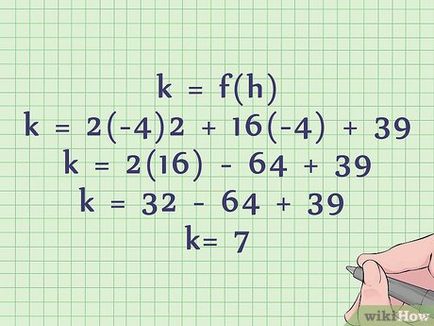
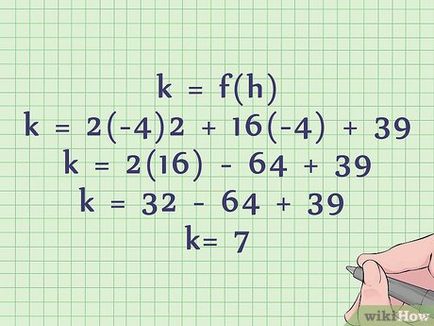
• Можете да откриете, че ч = -4 (за стандартния уравнение). За да се изчисли к заместител на тази стойност, вместо на "Х":
  • к = 2 (-4) 2 + 16 (-4) + 39.
  • к = 2 (16) - 64 + 39.
  • к = 32-64 + 39 = 7
• В нестандартен уравнение к = 12.

Нанесете топ координати (З, K) на координатната равнина. ч се нанася по оста X, и к - Y. В горната част на оста на парабола е или най-ниската точка (ако парабола сочи нагоре), или най-горната точка (ако парабола надолу).

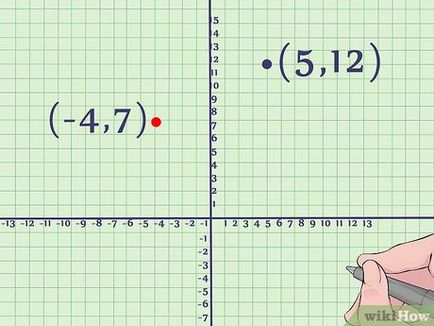
• В нашия пример, стандартната връх уравнение има координати (-4, 7). Приложете тази точка на координатната равнина.
• В този пример, връх обичай уравнение има координати (5, 12). Приложете тази точка на координатната равнина.

Извършва се ос на симетрия на параболата (не е задължително). Оста на симетрия преминава през върха на успоредно на парабола да Y ос (т.е. вертикално). оста на симетрия на параболата разделя наполовина (т.е. огледало парабола симетричен спрямо тази ос).

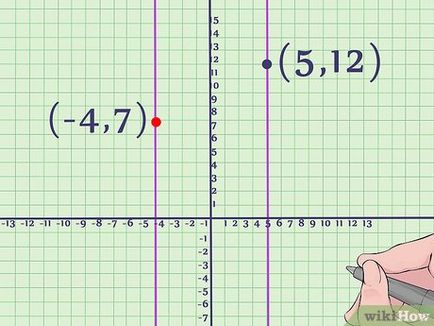
• В нашия пример, стандартната уравнение симетрия ос е линия, паралелна на оста Y и минаваща през точка (-4, 7). Въпреки, че тази линия не е част от самата парабола, тя дава представа за симетрията на параболата.

Определя парабола посока - нагоре или надолу. Много е лесно да се направи. Ако коефициентът "а" е положителен, парабола, насочена нагоре, и ако коефициентът "а" е отрицателен, параболата е насочен надолу.

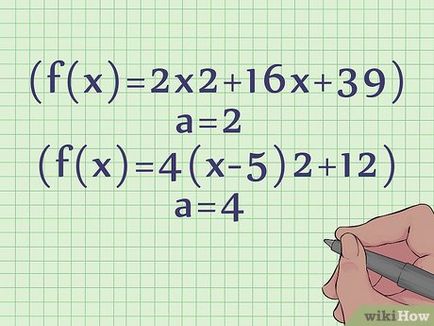
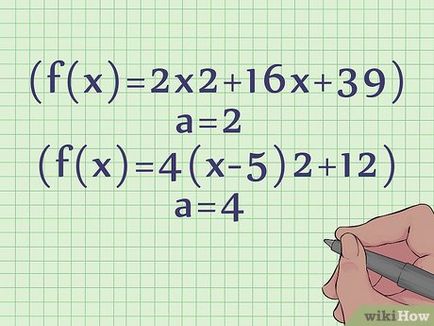
• В нашия пример, стандартната уравнение е (х) = 2 х 2 + 16x + 39 параболата сочи нагоре, като = 2 (положителен коефициент).
• В този пример, обичай уравнение е (х) = 4 (х - 5) 2 + 12 парабола и насочена нагоре, като = 4 (положителен коефициент).

Ако трябва да се намери и да прилага по отношение на точката на X-ос пресичане Тези точки в голяма степен ще ви помогнат в изграждането на парабола. Може да има два, един или никой (ако парабола нагоре и връх лежи над Х-ос, или ако параболата е насочен надолу, и неговия връх лежи под оста X). За да се изчисли координатите на точките на пресичане с оста Х, изпълнете следните стъпки:

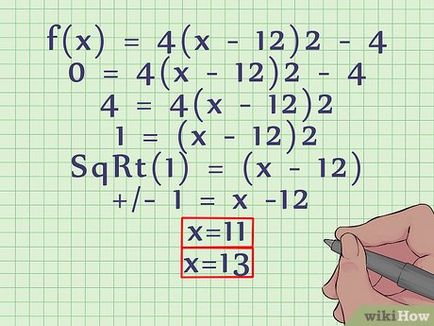
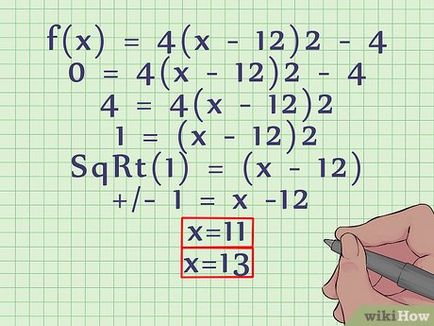
• Равнява уравнение на нула: е (х) = 0 и решаване. Този метод работи с прости квадратно уравнение (особено нестандартен тип), но може да бъде изключително трудно в случай на сложни уравнения. В нашия пример:
  • е (х) = 4 (х - 12) 2 - 4
  • 4 = 0 (х - 12) 2 - 4
  • 4 = 4 (х - 12) 2
  • 1 = (х - 12) 2
  • √1 = (х - 12)
  • +/ -1 = х -12. Точките на пресичане на парабола с координатите на оста X. са (11,0) и (13,0).
• Разтвори квадратно уравнение на стандартна форма фактори: брадва 2 + BX + с = (DX + д) (FX + г), където DX х FX ​​= брадва 2. (DX х грам + FX х д) = BX, д х G = в. След това се равнява на всеки биномиално до 0 и да намерят стойностите на "х". Например:
  • х 2 + 2х + 1
  • = (X + 1) (х + 1)
  • В този случай съществува уникална точка на пресичане на парабола с X оста на координатите (-1.0), защото, когато х + 1 = 0 х = 1.
• Ако не може да се разлага в уравнение фактори, да реши да използва формулата за изчисляване на квадратни корени на уравнението: х = (Ь +/- √ (б 2 - 4ав)) / 2а.
  • Например: -5x 2 + 1x + 10.
  • х = (-1 +/- √ (1 2 - 4 (-5) (10))) / 2 (-5)
  • х = (-1 +/- √ (1 + 200)) / - 10
  • х = (-1 +/- √ (201)) / - 10
  • х = (-1 +/- 14,18) / - 10
  • х = (13,18 / -10) и (-15.18 / -10). Точките на пресичане с параболи оста х имат координати (-1,318,0) и (1,518,0).
  • В нашия пример, стандартната уравнението на формата 2x 2 + 16x + 39:
  • х = (-16 +/- √ (от февруари 16-4 (2) (39))) / 2 (2)
  • х = (-16 +/- √ (256-312)) / 4
  • х = (-16 +/- √ (-56) / - 10
  • Тъй като корен квадратен от отрицателно число е невъзможно, тогава параболата не пресичат оста X.

Ако трябва да се намери и да прилага по отношение на точка Y. на оста пресичане Много е лесно - заместител х = 0 в оригиналния уравнение и намиране на стойността на "Y". В точката на пресичане с оста Y винаги е един. Забележка: в уравненията на формата на стандартната пресечната точка има координати (0, S).

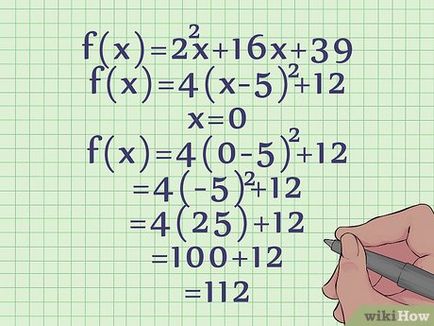
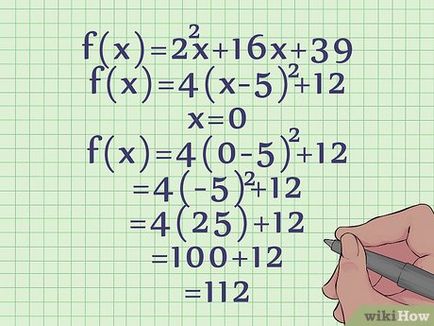
• Например, парабола квадратно уравнение 2 х 2 + 16x + 39 пресича оста Y в точка с координатите (0, 39) като с = 39. Но е възможно и да се изчисли:
  • е (х) = 2 х 2 + 16x + 39
  • е (х) = 2 (0) 2 + 16 (0) + 39
  • е (х) = 39, т.е. квадратно уравнение на параболата пресича оста Y в точка с координатите (0, 39).
• В този пример, нестандартни форма на уравнение 4 (X - 5) 2 + 12 пресичане с оста Y се изчислява както следва:
  • е (х) = 4 (х - 5) 2 + 12
  • е (х) = 4 (0 - 5,) 2 + 12
  • е (х) = 4 (-5) 2 + 12
  • е (х) = 4 (25) + 12
  • е (х) = 112, което е с квадратно уравнение на параболата пресича оста Y в точка с координатите (0, 112).

Намерили сте (и приложни) връх на параболата, посоката и точката на пресичане с брадви X и Y. на Можете да създадете парабола през тези точки или да намерят и да прилагат допълнителни точки и след това да се изгради парабола. За този заместител някои стойности "х" (от двете страни от върха) в оригиналната уравнение за изчисляване на съответните стойности на "Y".

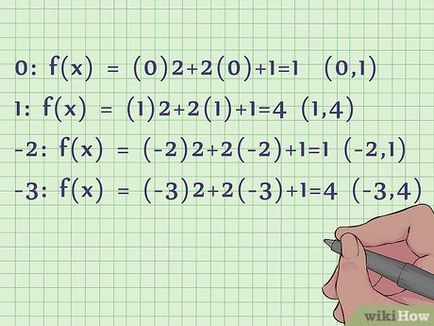
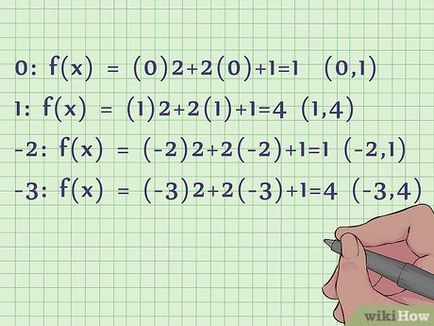
• Нека се върнем към уравнението х 2 + 2х + 1. Вече знаете, че точката на пресичане на графиката на това уравнение с оста Х е точката с координати (1,0). Ако параболата има само една пресечна точка с оста Х, който е на върха на параболата се намира на X. ос В този случай, една точка е недостатъчен за правилното изграждане на параболата. Така че отделете няколко допълнителни точки.
  • Нека х = 0, х = 1, х = -2, х = -3.
  • х = 0: е (х) = (0) 2 + 2 (0) + 1 = 1. Координатите на точката (0,1).
  • х = 1: е (х) = (1) 2 + 2 (1) + 1 = 4. Координатите на точката (1,4).
  • -2 х =: е (х) = (-2) 2 + 2 (-2) + 1 = 1. Координатите на точката (-2,1).
  • -3 х =: е (х) = (-3) 2 + 2 (-3) + 1 = 4. Координатите на точката (-3,4).
  • Нанесете точка на координатната равнина и изграждане на парабола (свързване точки U-образни криви). Моля, имайте предвид, че параболата е абсолютно симетричен - всяка точка на един клон на параболата да флип (по отношение на оста на симетрия) в другия клон на параболата. Това ще ви спести време, защото не е нужно да се изчисли координатите на точки от двете разклонения на параболата.