Как да намерите областта на диагоналната част на куба

Площта на диагоналната част на куб е много лесно да се намери, ако знаете стойността на ребрата, или площта на едно лице.

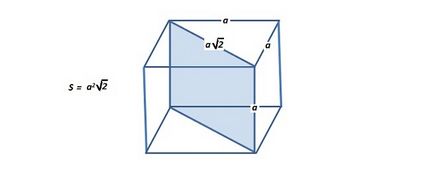
Ако известна стойност на ръба на куб, след зоната на напречното сечение открити по формула

S (диагонален разрез) = 1.414 * а * а *

Ако знаете, че площта на едно от лицата на куба, а след това формулата на зоната на куб сечение ще изглежда така

S (диагонален разрез) = 1414 * S (куб лица)

Забележка - за удобство, вместо на основата на два своето писмено числена стойност се закръглява към хилядна.

модератор избра най-добрият отговор

Axial напречно сечение на куба е правоъгълник, едната страна на който е равна на дължината на реброто, а другият - изправят диагонал. Ако ръба е известен и равно на. Тогава диагонални аспекти е едновременно равностранен хипотенуза на правоъгълен триъгълник, чиито крака са - това е две съседни ръбове на куб или две страни на квадратен лицето. Следователно диагонал (хипотенуза) може да се изчисли от Питагоровата теорема, дължина или ребро и съотношението на 45grad задължително (или косинус) (половината от прав ъгъл). Синусите 45grad равна на половината от площада. корен от 2 или 0,707. Следователно, диагонал В = а / 0.707. И областта на диагонала на квадрат сечение:

S = A * б = (а ^ 2) /0.707

(Когато ^ 2 - е квадратна, или във втората степен).

Намирането на квадратен диагоналната част на куба не е сложна задача, защото куба всичките му страни са равни, а лицата са квадрати. Ето защо, ако се построи куб сечение, минаваща през диагонално противоположни страни, ние получаваме правоъгълник, където по-малките страни, изглежда, равни на куба, нека да бъде класически, така и дългите страни, ще бъде равна на дължината на диагонала на квадрат със страна А.

Формулата за намиране на диагонали тук:

Площта на правоъгълник - е продукт на своите страни, и след това формулата на квадрата на диагонална част на куба е под формата: