Изследвания в математика геометрия на кръгове

Продължаване за изчисление действия във връзка с 3072-гон, намери по-точно приближение на десетична дроб е равно на 3.14159.

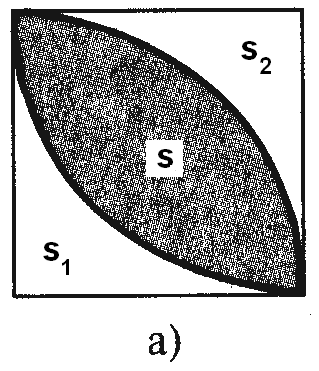
На страните на правоъгълен триъгълник като диаметри извън построени полукръговете. Докажете, че площта на полукръга, построен върху хипотенузата е равна на сумата от областите на полукръгове, изградени върху Catete.

Ние показваме, че S = S1 + S2. Нека един от краката на правоъгълен триъгълник е равен на х, а другият крак е в, а след това на хипотенузата е равен на питагорова теорема

Намери S1. Тъй S2 и S. радиус на първия кръг е равна на х / 2 и радиуса на втори кръг е равна на у / 2, и радиусът на третия кръг е,

S1 + S2 = + =. QED.
Проблем № 2.

Даден е квадрат със страна, равен на 1. Намерете областта на сенчестата фигурата.

Решение: Нека да се намери квадрат площ: S = 1.

Площ S + S1 = ¼ квадрат до радиуса на кръга, равен на 1.

Намираме ¼ кръг площ: S + S1 = / 4

площ Naodom S2 = площ на квадрат - зоната S + S1

За да намерите областта на сенчестата фигура, изважда областта на квадрат площ от S1 и S2. Получават: S = 1-2 (1- / 4) = 1-2 + / = 2 / 2-1.

Arc окръжности, правилен многоъгълник, ограничаващи страна, се показват симетрично по отношение на тези страни. Търсене за:

1) Зоната попълнено форми ако страна на многоъгълника е равно на 1;

2) Намерете лицето на форма, подобна на равностранен петоъгълник; прав п - гон.

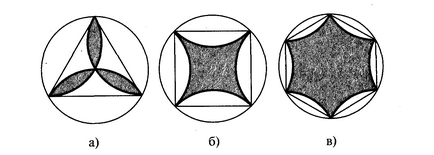
Отговор: 1) Площ trohlepestkovoy фигура е разликата между площта на тройната кръгов сегмент и зоната на триъгълник. Три пъти площта на кръгов сегмент, равна на разликата между площта на кръга и зоната на триъгълник. По този начин, необходимата площ е равна.

2) Площта на защрихованата фигура равен на разликата между два пъти площта на многоъгълник и зоната на кръг.

ох

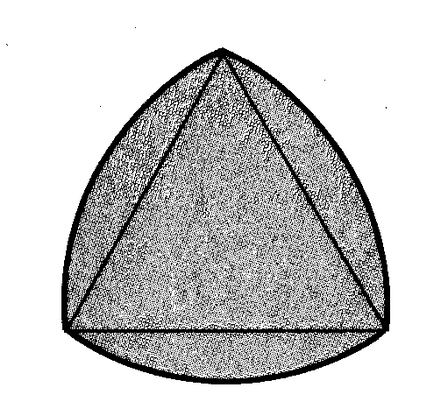
Коло квадрат със страна 1, описан кръг, и неговите страни като диаметри построен полукръг. Намерете лицето на защрихованата фигура.
Отговор: 1.

P

Ostrow три дъги от окръжности с центрове и завършва с една страна на равностранен триъгълник върховете 1. Виж областта на получената форма.

Н

и страните А, В, правоъгълен триъгълник като диаметри конструирана кръг. Намерете лицето на защрихованата фигура.

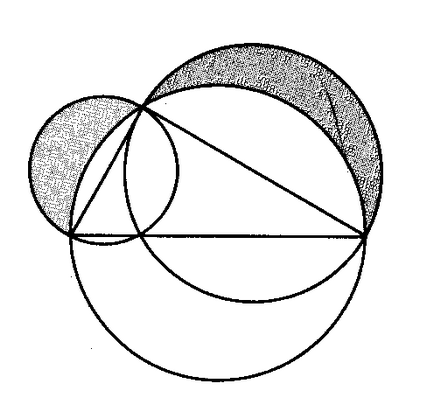
отговори на:

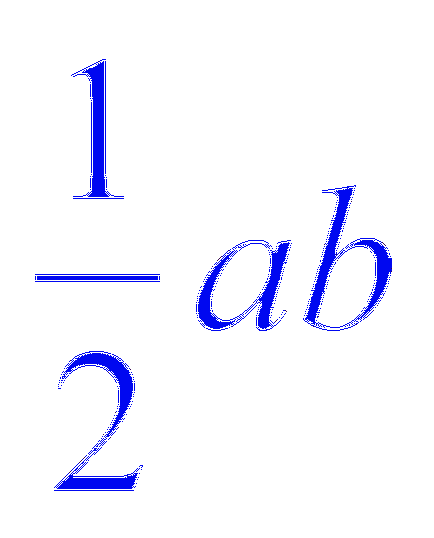
WАдачи № 7.

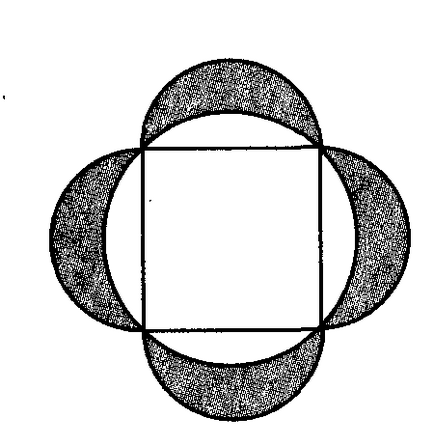
Диаметър 2R обиколка разделена на четири равни сегменти. При получаване на сегментите са конструирани полукръг. Изчислете областта на пълни фигури. Изчисляват дължина на всеки контур сенчеста форма.

W

там кръгове на еднакъв радиус R докосват кръга на същия радиус и по двойки един до друг. Що се отнася до пръстен от шест кръгове, и областта е площта на седемте кръгове на данни. Намерете широчината на пръстена.

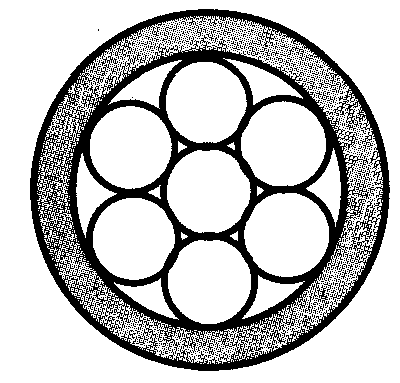
Три равни кръгове връзка помежду си и радиуса на окръжност R. намерят своето радиуси. Решаване на този проблем в продължение на четири, пет, осем кръга.

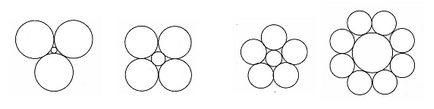
Отговор: радиусът на кръга х може да се намери от уравнението , където п - брой на кръгове.

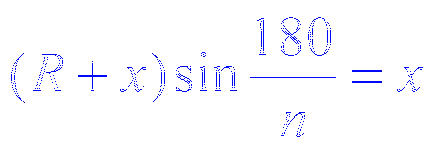
Най-

триъгълник вписан кръг с радиус R допирателни успоредни на страните на триъгълника. триъгълници отрязани допирателните на вписан кръг радиусите R1, R2 и R3. Докаже, че R1 + R2 + R3 = R.

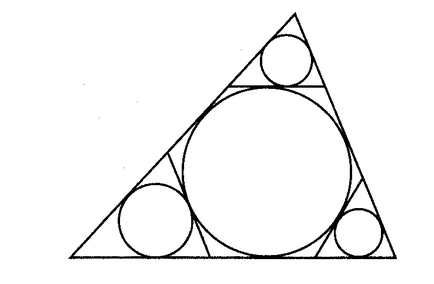
Мислено извършвате тази процедура с всяка от трите подрязани триъгълници, и така нататък. D. Намерете сумата от радиусите на получените кръгове на всеки етап.

Отговор: Ако си ха. HB. HC - височина на триъгълник, съответните височини на малки триъгълници ще бъде равен ха -2R, HB -2R, ж.к. -2R. От сходството на триъгълници намери тази сума отношения, като се заменят със съотношение на височината.

Изследвания по Математика Тема: "Magic триъгълник"