Изчисляване на разстоянието между две линии и координира всички общи перпендикулярна

Координати всички общи перпендикулярна два пропускателни или пресичащи се линии.

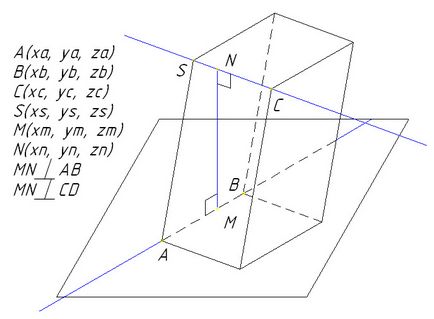
В предоставеното му пространство четири точки:

Линии AB и CS са кос или се застъпват.






Намерете координатите на всички по-често перпендикулярно линии АВ и ВС на

Нека пет условия:

1. точка М (х, YM, ZM) принадлежи към права линия AB;
2. Точка N (Xn, ин, Z6) принадлежи към една права линия CS;
3. Директен MN перпендикулярно на линията AB;
4. Директен MN перпендикулярна линия CS;
5. Линии AB и CS не са успоредни;

След това сегмент [МН] е общо перпендикулярна на линиите АВ и CS. и дължината на интервала [МН] е най-късото разстояние между правите линии АВ и CS.

Извършва пет след пет условия:

Координати паралелни (колинеарни) вектори са пропорционални.

В скаларен продукт на перпендикулярни (ортогонални) вектори е нула.

Колинеарни векторите на вектор продукт не е равна на нула вектор. Модулът на вектор продукта от не-колинеарни вектори стриктно по-голяма от нула.

По предположение, тъй като линии АВ, и CS не са успоредни, векторната продукта

, Следните пет условия:

Ние изразяваме XM от първите две уравнения. YM. ZM. хп. ин. Zn

Намираме координатите на вектор MN:

Заместването на х. YM. ZM. хп. ин. Zn в третото и четвъртото уравнение, ние откриваме на М и Н:

Качваме се на система от две уравнения с две неизвестни м. п.

Имаме следната система от две уравнения с две неизвестни м. п:

От площада на вътрешния продукт на не-колинеарни вектори винаги строго по-малко от продукта от квадратите на модулите на тези вектори, в основния фактор за тази система:

Ето защо, тази система има уникално решение.

Координати всички общи перпендикулярна [МН] на двата кос линии. Сегментът [МН] е перпендикулярна на AB и перпендикулярна SC

Координатите на точка М (х, YM, ZM). лежи на линията AB:

Координатите на точка N (хп, ин, Zn). лежи на SC линия.

Координати всички общи перпендикулярна на кос (или кросоувър) Директен КБ и CS:

Разстоянието между неуспоредни прави линии.

Два начина за изчисляване на разстоянието между които не са успоредни прави линии.

Разстоянието между неуспоредни прави линии AB и НС могат да бъдат открити по формулата:

Разстоянието между неуспоредни прави линии AB и НС може да се намери втори начин височината на паралелепипед база, чиито страни са [AB] и [SC]. и странично ребро е [AS].

Чрез изместване на началната точка на вектора в SC А. ще изгради една кутия на векторите AB. SC. AS. чийто обем е равен на модула на смесен продукт AB вектори. SC. AS. базова площ равна на модула на вектор продукта от вектори AB и SC. Разстоянието между редовете АВ и НС равна на височината на паралелепипеда конструирана на векторите AB. SC. AS.

Vector продукт AB и SC има координати:

Модул вектор продукт на вектори AB и SC.

Модул AS смесени вектори на продукта. AB. SC:

Най-късото разстояние между линиите АВ и CS може да се намери от формулата:

Разстоянието между успоредни линии AB и CS

Разстоянието между успоредните линии AB и CS е разстоянието от точка S (х, YS, ЗС) на линията AB.

Има и два начина за намиране на разстоянието между две успоредни линии, т.е. два начина за намиране на разстоянието от точката на ред. На първо място, ние откриваме, координатите на точката за проекция на линията. Директен AB се дава координатите на две от неговите точки

Точка К е проекцията на точка S върху линията AB.

Намерете координатите на точка К

За да намерите координатите на условията за употреба, буква К:

1. Вектори AK и AB - лежат на една права, техните координати са пропорционални;
2. Вектори и SK AB са ортогонални и тяхното скаларен продукт е нула;

От първото уравнение

Заместването XK. ук. жк в второто уравнение, ние намеря:

Координатите на точка S на проекция на линия AB. т.е. координатите на точка К (XK, ук, ЗК):

Разстоянието между точка S и права линия AB могат да бъдат открити по формулата:

Разстоянието между точката S и права линия AB а може да се намери втори начин, като височината на успоредник, стените на който са [AB] и [AS].

вектор продукта от вектори AB и като има координати:

Модул вектор продукт на вектори AB и AS:

Големината на КБ:

Разстоянието между точка S и права линия AB могат да бъдат открити по формулата:

Програмата "Изчисляването на разстоянието между две линии и координира всички общата перпендикуляра."

Програмата "Изчисляването на разстоянието между две линии и координира всички общата перпендикуляра."

Издадена текущата координатна стойност координира всички общи перпендикулярно на линии АВ и ВС като несводима рационално фракция в / R.
Издадена текущата стойност разстояние между две линии под формата на С * SQRT (р) / г

Фракция в / г е неизлечим рационално фракция и р radicand експресия не съдържа техните делители квадрати естествени числа.

Резултатът може да се показва във файла.

За да преместите курсора към следващото поле и изчисляване на резултатите, използвате клавиша Enter.