Изчисляване на площ на фигурата е показано на милиметрова хартия
В подготовката си за основния държавен изпит, се запознах с дейности, които изискват изчисли площта на фигурата е показано на кариран лист хартия. Като правило, тези задачи не водят до големи трудности, ако цифрата е трапец, успоредник или триъгълник. достатъчно добре, за да се знае, формулите за изчисляване на областите на тези цифри, както и да отчита броя на клетките, за да се изчисли района. Ако цифрата е произволна полигон, че е необходимо да се използват специални техники. Интересно ми беше в тази тема. И разбира се на всички въпроси: къде в ежедневието може да бъде проблем при изчисляването на площите, засети с милиметрова хартия? Какво е специалното на тези проблеми? Има ли и други методи или универсална формула за изчисляване на площта на геометрични фигури, изобразени върху милиметрова хартия?
Като се има предвид правоъгълна координатна система. Ние считаме, многоъгълник, който има целочислени координати в тази система. В научната литература точки с целочислени координати се наричат възли. И на полигона не е необходимо да бъде изпъкнал. И нека това да се изисква да се определи неговата област.
Следните случаи.
1. Цифрата е триъгълник, успоредник, трапец:
1) преброяване на клетките трябва да се намери височината, диагонал или лица, които са необходими за изчисляване на площта;
2) замести стойността намерени в формула област.
Например, е необходимо да се изчислява площта на фигурата е показано на Фигура 1, на размера на клетките единcm една cm.
Фиг. 1. Триъгълник
Решение. Разчитаме на клетките и да намерят това. Според формулата получаваме :.
Фигура 2 е многоъгълник
Ако формата е многоъгълник е възможно да се използват следните методи.
1) се разделят на многоъгълника на триъгълници, правоъгълници;
2) изчисляване на стойностите на площ получени;
3) Виж сумата от всички области на получената форма.
Например, е необходимо да се изчислява площта на фигурата е показано на Фигура 2 с размер на клетка на един сантиметър от един сантиметър дял.
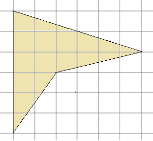
Фиг. 2. Polygon
Решение. Partition, има много начини. Ние се разделят на фигурата в правилните правоъгълен триъгълник и правоъгълник, както е показано на фигура 3.
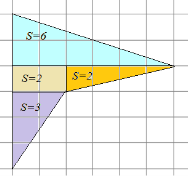
Фиг. 3. полигон. метод за разделяне
Области на триъгълници са равни: ,,, площ на правоъгълника -. Сгъваеми площ от всички цифри, които получаваме:
Методът за изграждане на допълнителен
1), за да продължи формата на правоъгълник
2) да се намери областта получи допълнителни цифри и площта на правоъгълника
3) от площта на правоъгълника да изважда областта на всички "екстра" парчета.
Например, е необходимо да се изчислява площта на фигурата е показано на Фигура 2 с размер на клетка на един сантиметър от един сантиметър допълнителна конструкция.
Решение. Ще приключим нашата форма на правоъгълник, както е показано на фигура 4.
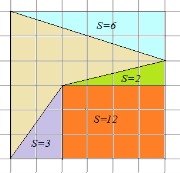
Фиг. 4. полигон. метод допълнения
Площта на голям правоъгълник е равно на правоъгълника се намира вътре - районът на "екстра" триъгълници - и след това желаната област на фигурата.
При изчисляване на площ от полигоните на хартия карирания възможно да се използва друг метод, който е известен като Теорема на Пик на името на учения, който го е открил.
Нека многоъгълник изобразен на милиметрова хартия само число връх. Точката, в която и двете координати са цели числа, наречени стълбове сайтове. Освен това, многоъгълник може да бъде изпъкнала или не-изпъкнала.
площ на полигон с цяло число, равно върхове, където B - номерът на целочислени точки от полигона, и F - броят на целочислени точки на границата на полигона.
Например, за многоъгълника е показано на фигура 5.
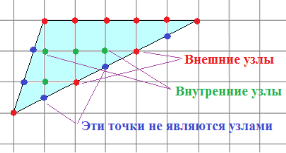
Фиг. 5. възли във формула връх
Например, е необходимо да се изчислява площта на фигурата е показано на Фигура 2 с размера на клетки 1cm 1см формула връх.
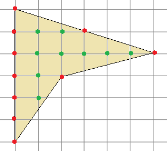
Фиг. 6. полигон. Теорема на Пик
Решение. Съгласно фигура 6: В = 9, Т = 10, тогава има формула пик:
1. детски деца от прилагане на родителите като подарък (Фигура 7). Намерете зоните на употреба. Размерът на всяка клетка е 1 cm 1sm.
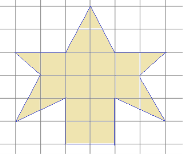
Фиг. 7. Състояние Задача 1
2. Един хектар смърчови насаждения може да забави една година до 32 тона прах, бор - до 35 тона, бряст - до 43 тона дъб - до 50 тона бук - .. До 68 т преброим колко тона прах ела закъснение от 5 години. план смърч е изобразен във Фигура 8 (скала от 1 см. -. 200 м).
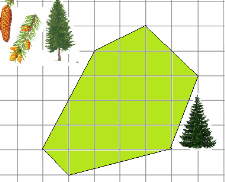
Фиг. 8. Състояние Задача 2
3. орнаменти Ханти и Манси, доминиран от геометрични мотиви. Често има стилизирани изображения на животни. Фигура 9 показва фрагмент Мансийск орнамент "заешки уши". Изчислете областта на сенчеста част на украшението.
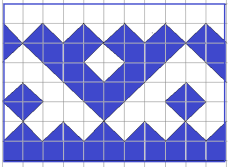

Фиг. 9. Състояние Задача 3
4. Задължително да рисува по стените на сградата на фабриката (фиг. 10). Изчислява се необходимото количество латекс бои (в литри). скорост мастило поток: 1 литър 7 кв. м мащаб 1 cm - 5м.
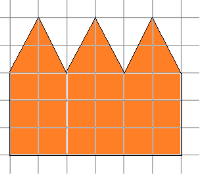
Фиг. 10. Състояние Задача 4
5. звездообразна многоъгълник - плосък геометрична фигура състои от триъгълни лъчи, идващи от общ център, сливащи се в точка на сближаване. Специално внимание трябва да бъде звезда с пет лъча - Пентаграм. Pentagram - символ на съвършенство, интелигентност, мъдрост и красота. Това е най-простата форма на звезди, които могат да бъдат представени само с един удар на писалката, никога не го премахнете от хартията и по този начин никога не еднакви, без да преминават два пъти на една и съща линия. Направи петолъчка без повдигане молива от листа на милиметрова хартия, така че всички краища на получената многоъгълника е в клетъчните възли. Изчислява областта на числото, получено.
След анализ на математическа литература и сортиране на голям брой примери за предмет на научни изследвания, аз стигнах до заключението, че изборът на метод за изчисляване на площта на фигурата на кариран хартия зависи от формата на фигурата. Ако формата е триъгълник, правоъгълник, успоредник, или трапец, че е подходящо да се възползвате от всички известни формули за изчисляване на площи. Ако формата е изпъкнал многоъгълник, то тогава е възможно да се използва като метод за разделяне и добавката (в повечето случаи е по-удобно - метод допълнения). Ако стойността е не-изпъкнал многоъгълник, или с форма на звезда, която е по-удобно да се прилага формула връх.
Тъй формула връх е универсален уравнение за изчисляване на области (ако върховете на многоъгълника са в решетъчни точки), може да се използва за всяка фигура. Въпреки това, ако полигон заема голяма площ (или малка клетка), тогава е вероятно да направи грешка в броенето на решетъчни възли. Като цяло, в хода на изследванията, дойдох до заключението, че в работата си с такива проблеми в СЕГ по-добре да се използват традиционните методи (разделяне или добавка), а резултатът се проверява от формула връх.
