формула продукт на синус, косинус и задължително и косинус

Изследване на основните формули на тригонометрични формули продължи работата задължително, косинус и задължително косинус. Тези формули са в известен смисъл обратен формули суми Sines и уют. тоест, да позволи на произведението на Синеш и уюта, и отидете на сумата или разликата на Синиш и уют и.

В тази статия, ние считаме, по следната формула: продукт на Синиш, косинуси на продукт и на синуса и косинуса, показват тяхното приключване, и да даде примери за тяхната употреба.

Навигация в страниците.

списък с формули

Пишем реда на продукт формула задължително, косинус и задължително косинус.

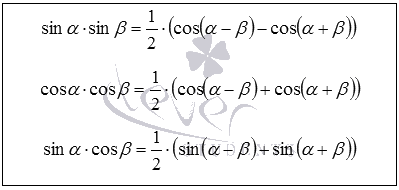
Тези формули са валидни за всички ъгли и.

Данните изрази формулировка продукт с формула:

• Продуктът на Синеш на ъгли и още половин косинус на ъгъла и косинус на ъгъла.
• Продуктът на уют и равен на половината от сумата на косинус на ъглова разлика и косинус и сумата на тези ъгли.
• Продуктът на синус и косинус на ъгъла на ъгълът е равен на половината от сумата и разликата на ъглите на синуса и синуса на сумата на тези ъгли.

Получаване на формули

Продукт формула синус, косинус и задължително и косинус могат да бъдат получени на базата на присъединителни формули. както и следните равенства имота. ако лявата и дясната страна на уравнението правилно да добавите левия и десния съответно на друго истинско равенство, ние получаваме истинско равенство.

За да се извлече формули продукт на Синиш и уют ние се нуждаем от сумата на косинус на формула и косинус вида и разликата.

Добавянето на тези равенства, ние получаваме от което следва, че. Така се оказа формула уют продукт.

Ако сумата от формулата за косинус пренаписана като след това, за да добавите това равенство между половете, а след това лесно се получава продукт формула задължително форма.

За получаването на синус и косинус продукт достатъчно, за да сгънете лявата и дясната страна на формули задължително сумата и разликата задължително. Ние имаме, от което следва, че.

Така че не сме внесли формулата продукт на синус, косинус и задължително и косинус.

примери за употреба

Нека да разгледаме някои примери за формули продукт на синус, косинус и задължително косинус. Това се прави, за да стане ясно, като се използват гледани формули за специфични ъгли.

Да започнем с това, проверката за валидност, например, продукт формули синусите. За това ние приемаме и се уверете, че едни и същи стойности на дясна и лява страна на тези ъгли. Имаме (ако е необходимо, направете справка с таблица на стойностите на синус, косинус, тангенс и котангенс) и

Тъй като ние имаме една и съща стойност, продуктът на задължително формула е валидна за дадените ъгли.

В някои случаи формулата на продукта може да се изчисляват стойностите на тригонометрични изрази. Помислете за един пример, който потвърждава нашите думи.

Изчислете точната стойност на продукта на синуса и косинуса на 75 градуса до 15 градуса.

Точните стойности са неизвестни за нас, така че не можем директно изчисляване на необходимата стойност. Въпреки това, отговорът на въпроса на проблема ни позволява да продукт формула на синус и косинус. Всъщност, сумата от ъглите 75 и 15 градуса е 90 градуса, а разликата между тях е 60 градуса, за което знаем точните ъгли на данните на стойностите на тригонометричните функции.

.

Каталог формула синус, косинус, синус и косинус функции се използват за преобразуване на тригонометрични изрази. но този въпрос изисква по-подробна дискусия.