Допирателната към графиката на уравнението на функциите на допирателната
Помислете за следната картина:
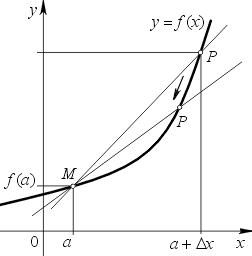
Това показва функция у = е (х) е диференцируема в точката на. Маркирано от точка М с координати (а; е (а)). Чрез произволна точка Р (а + Δx; е (а + Δx)), генерирани извършва сечащ MR.
Ако сега точка Р на графика за смяна на точка M, а след това на линията LL ще се върти около тази точка М. Когато АН ще са склонни към нула. От това можем да се формулира дефиницията на допирателната към графиката на функцията.
Допирателната към графиката на функцията
Допирателната към графиката на функцията има крайно положение на напречното сечение клони към нула нарастване на аргумента. Трябва да се разбере, че наличието на производно е в x0 означава, че в този момент графиката е допирателна към него.
Ъгловата коефициента на допирателната е равна на производно на функцията на точка F "(x0). Това е геометричното значение на производно. Допирателната към графиката в точка x0 диференцируеми функции F на - е линия, минаваща през точка (x0; F (x0)) и имащи ъглова коефициент F '(x0).
Уравнението на допирателната
Нека да се опитаме да се получи уравнението на допирателната към графиката на функция е в точка A (x0; F (x0)). уравнение на линия с наклон к е както следва:
Тъй като ние имаме наклон равен на производно F '(x0). уравнението се следната форма: у = F '(x0) * х + б.
Сега ние се изчисли стойността на б. За това ние използваме факта, че функцията минава през точка А.
F (x0) = F '(x0) * x0 + б, б и следователно изразяват получи б = F (x0) - F' (x0) * x0.
Замени стойността, получена в уравнението на допирателната:
Y = F '(x0) * х + б = F' (x0) * х + F (x0) - F '(x0) * x0 = F (x0) + F' (x0) * (х - x0).
Y = F (x0) + F '(x0) * (х - x0).
Да разгледаме следния пример: намерите уравнението на допирателната към графиката на F функция (х) = х 2 - 3 * х 2 + 1 при х = 2.
2. F (x0) = F (2) = 2 2 - 2 * 2 2 + 1 = 1.
3. F '(х) = 3 * х с 2 - 4 * х.
4. F '(x0) = F "(2) = 3 * 2 2 - 4 * 2 = 4.
5. Заместването на получените стойности във формулата на допирателната, ние получаваме: у = 1 + 4 * (х - 2). Разширяване на скобите и цитиране подобни термини се получат: Y = 4 * х - 7.
Общата схема на получаване на уравнението на допирателната към графиката на у = е (х):
1. Определете x0.
2. Изчисли F (x0).
3. Изчисли F '(х)
4. Изчисли F '(x0)
5. Заместването стойностите в уравнението на допирателната Y = F (x0) + F '(x0) * (х - x0).