проект "дивизия с остатък"
Участък с остатък
Тя не винаги е едно число, могат да бъдат напълно отделени в друго. Разделянето в Примери остатък може да остане. Такова разделяне се нарича разделяне с остатък.
Участък с остатък - това разделяне на един брой от друг естествено число, в която остатъкът не е нула.
Ако до края на разделението на естествените числа е нула, ние казваме, че дивидентът, разделено на делителя без остатък, или, с други думи, се дели.
Участък с остатък се записва, както следва:
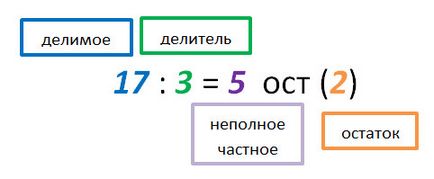
Виж примера, както следва:
17 ще бъдат разделени от 3 и 5 2 остатък.
Процедурата на примери за решения разделяне с остатък.
Ние считаме, най-много до 17, която е разделена на три без остатък. Този 15.
Ние се изважда от дивидента на числото, получено в стъпка 1.
Сравнете остатък разделител.
Когато дивизия с остатък остатък трябва винаги да бъде по-малко от делителя.
Ако се оказа, че повече от останалата част на разделителя, тогава вие сте наред да намери най-голям брой, че е разделен с делителя без остатък.
В решаването на по-сложни примери не винаги са лесни за намиране на най-голям брой точки 1. Понякога е необходимо да се правят допълнителни изчисления в колона. Ние показваме това, като един пример.
Методът на избор, за да се намери колко е необходимо да се умножи по 27, за да получите броя до най-близкия 190.
Нека се опитаме да се умножи по 6.
Остатък изчисли и да я сравни с разделител.
Балансирайте върху разделителя. Това означава, че 6 като множител не ни допадна. Нека се опитаме да се размножават разделителя 7.
Отново, ние се изчисли и сравни остатъка с делителя.
Остатъкът беше по-малък от делителя. Така един пример решен правилно. Ние напишете отговора.
190. 27 = ограничителя 7 (1)
Всички изчисления по-горе могат да бъдат представени под формата на дълъг участък. Правилник за разделение, можете да освежаване на урок "дълго разделение" на нашия уебсайт.
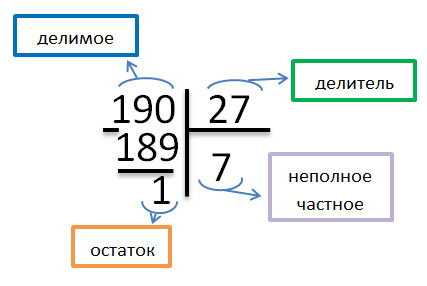
Как да проверите деление с остатък
Частичното отношението, умножено по делител
Добавено към резултат полученият остатък
Сравнете това с резултат се дели
Проверяваме отговора в нашия пример.
190. 27 = ограничителя 7 (1)